Part H. Channel Sounding
1. Channel Sounding physical channels
Channel Sounding (CS) defines 79 RF channels in the 2.4 GHz ISM band and defines a new channel index for each of these channels. Table 1.1 shows the relationship between CS channel indices and RF center frequency. Table 1.1 also shows some of the CS channel indices are not allowed for CS communication.
CS Channel Index | RF Center Frequency | Allowed |
|---|---|---|
0 | 2402 MHz | No |
1 | 2403 MHz | No |
2 | 2404 MHz | Yes |
… | … | … |
22 | 2424 MHz | Yes |
23 | 2425 MHz | No |
24 | 2426 MHz | No |
25 | 2427 MHz | No |
26 | 2428 MHz | Yes |
… | … | … |
76 | 2478 MHz | Yes |
77 | 2479 MHz | No |
78 | 2480 MHz | No |
2. Packet formats for Channel Sounding
CS uses a specific modulated bit sequence known as CS_SYNC. The CS_SYNC packet format is similar to a packet format for LE Uncoded PHY, except that the CS_SYNC packet has no PDU, CRC, or CTE fields. The format of the CS_SYNC packet is shown in Figure 2.1.

The preamble is 8 bits when transmitting or receiving on the LE 1M PHY and 16 bits when transmitting or receiving on the LE 2M and the LE 2M 2BT PHYs. The CS Access Address is 32 bits. The trailer is 4 bits. The Sounding Sequence and Random Sequence fields are optional. If present, the Sounding Sequence field shall be of length 32 or 96 bits. If the Random Sequence field is present, it shall be of length 32, 64, 96, or 128 bits.
The variable length of the optional Sounding Sequence and Random Sequence fields allows an implementation to optimize the total packet length versus the correlation accuracy of the field. CS packets with no Sounding Sequence or Random Sequence fields take 44 µs to transmit when sent using the LE 1M PHY and 26 µs to transmit when using the LE 2M and the LE 2M 2BT PHYs. CS packets that include a Sounding Sequence or Random Sequence field take longer to transmit based on the length of the field and the PHY selection.
2.1. Preamble
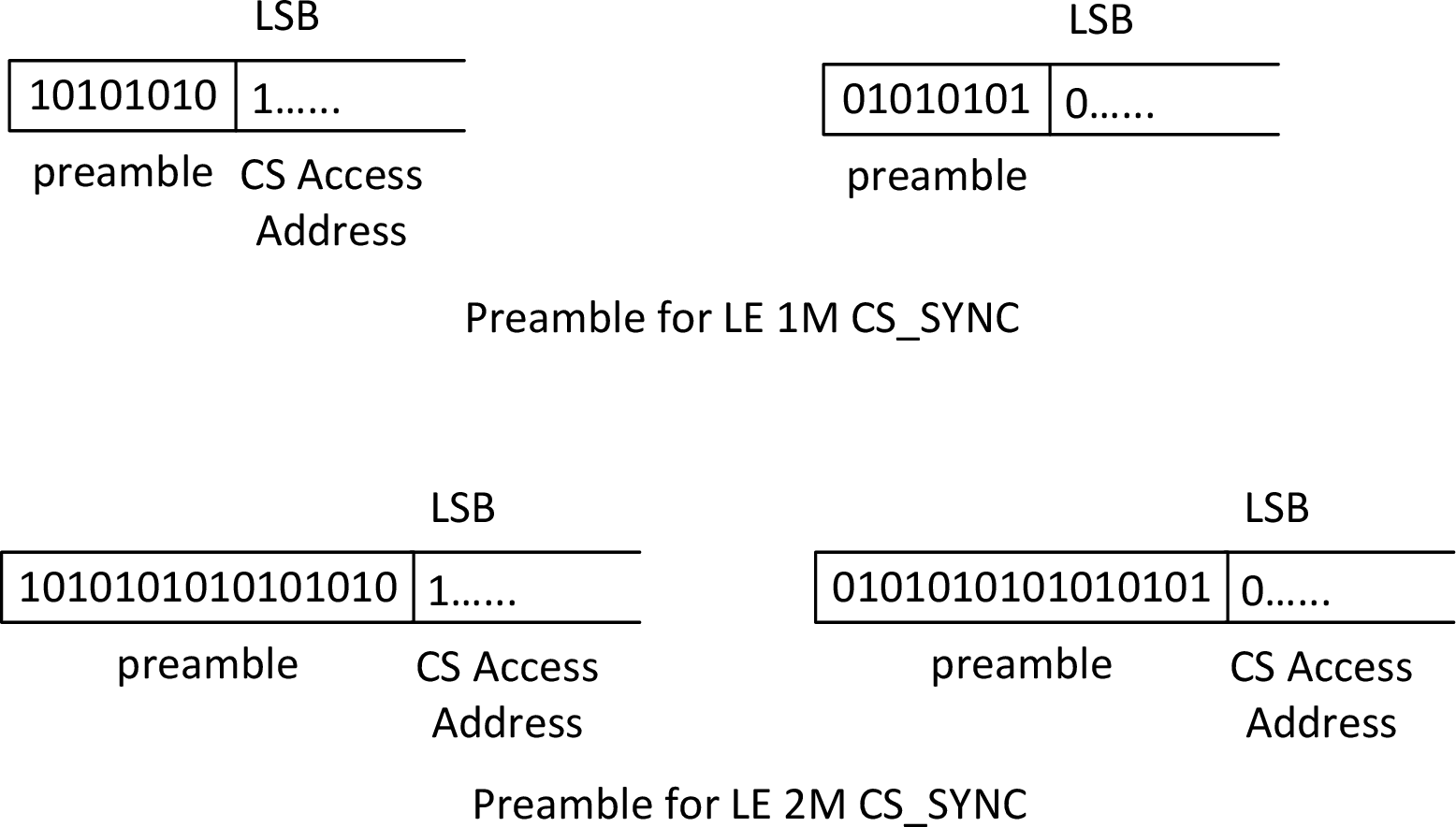
The same rules defined for the preamble of the LE Uncoded PHY packet format as described in [Vol 6] Part B, Section 2.1.1 shall apply to the preamble of the CS packet format. The preamble for CS_SYNC is shown in Figure 2.2.
2.2. Channel Sounding Access Address
Each CS Access Address is a sequence of bits that shall be cryptographically generated using the CS DRBG described in [Vol 6] Part E, Section 3.1.6. Devices that communicate with CS shall generate a common set of CS Access Addresses using the CS Access Address selection rules described below. The CS Access Addresses are used for synchronization, security, and round-trip time purposes.
Each CS step that transmits a CS_SYNC packet requires two CS Access Addresses that are derived from four DRGB output vectors of 32 bits each. The four vectors form four bit sequences s0, s1, s2, and s3 in the order the vectors were generated. Each bit sequence is constructed directly from the ordered bit output from the DRGB, with the first bit from the DRGB forming bit 32 (the most significant bit) of the sequence, the second bit forming bit 30, and so on, with the final bit forming bit 0 (the least significant bit) of the sequence. This ordered bit assignment is shown in Figure 2.3.

Sequences s0 and s1 are fed into the CS Access Address selection rules to produce a 32-bit sequence that becomes the CS Access Address of the first part of the CS step. Similarly, sequences s2 and s3 are fed into the CS Access Address selection rules to produce a 32-bit sequence that becomes the CS Access Address of the second part of the CS step.
The CS Access Address is transmitted least significant bit first (i.e., from bit 0 to bit 31).
2.2.1. Channel Sounding Access Address selection rules
The CS Access Address selection rules determine which of the two 32-bit candidates is selected to become the CS Access Address. These two 32-bit values shall be generated using the CS DRBG described in Section 4.8 at the step that requires the RTT exchange. The two random 32 bits for the CS Access Address candidates used in the CS_SYNC from the initiator to reflector shall be generated first. These two 32-bit values are referred to as s0 and s1 per the notation in Section 2.2. The two random 32 bits for the CS Access Address candidates used in the CS_SYNC from the reflector to the initiator shall be generated second. These two 32-bit values are referred to as s2 and s3 per the notation in Section 2.2. Filtering rules assign one autocorrelation score to each pair of 32-bit candidates. The sequence with the lower autocorrelation score is selected as the CS Access Address. If both sequences achieve the same autocorrelation score, then the second of the sequence pair (i.e., s1 and s3) shall be selected.
The CS autocorrelation score is a function that applies to a 32-bit sequence that is composed of 32 individual bits si (i in the 1 to 32 range) and is defined as:
Where each of the Ck elements is defined as:
2.2.2. Channel Sounding Access Address checking
A device shall return a CS Access Address quality indication value, as shown in Table 2.1, for a CS_SYNC packet received or intended to be received in a CS step. Although the generation of an Access Address quality indication value is implementation specific, the meaning noted in Table 2.1 should be followed. Only packets with an Access Address quality indication value of 0 shall be used for testing RTT accuracy measurements.
Value | Meaning |
|---|---|
0 | CS Access Address check is successful and all bits match the expected sequence. For non-Mode‑0 packets, the device has obtained a ToA‑ToD (or ToD‑ToA) measurement from the packet. |
1 | CS Access Address check contains 1 or more bit errors. For non-Mode‑0 packets, the device has obtained a ToA‑ToD (or ToD‑ToA) measurement from the packet. |
2 | CS Access Address not found |
3 | RFU |
2.3. Trailer
The CS trailer is a sequence of 4 bits, alternating between 0 and 1 bits. As shown in Figure 2.4, the trailer is 1010 (in transmission order) when the most significant bit of the CS Access Address is a 0, and 0101 when the most significant bit of the CS Access Address is a 1.

2.4. Sounding sequence
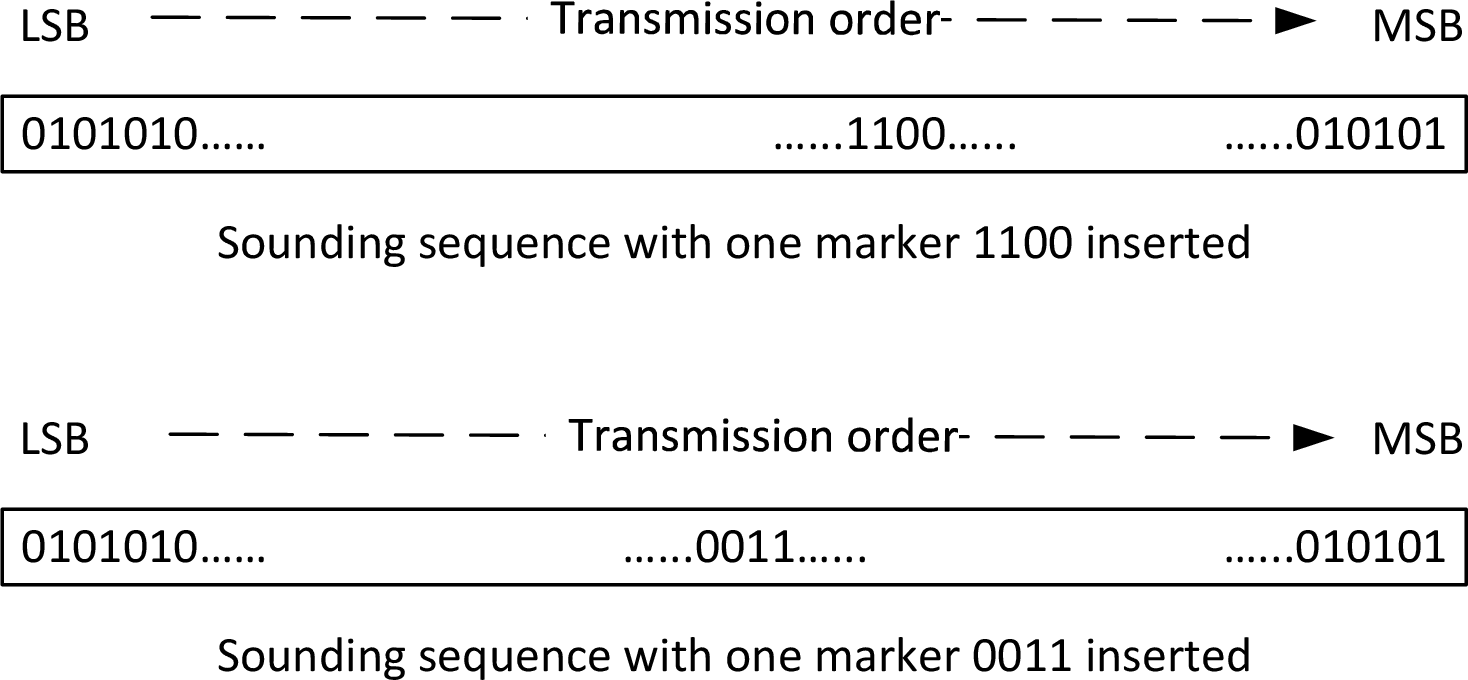
The optional sounding sequence is a sequence of bits alternating between 0 and 1, starting with a 0 as the first bit (LSB) in transmission order, which is then partially overwritten by one or two marker signals for resilience against spoofing attacks. Both the marker signal position and bit pattern are selected separately for each CS_SYNC transmitted.
The marker signal is 4 bits long. There are two possible signals that are selected randomly, seeded by the CS DRBG as described in Section 4.8. CS DRBG shall be invoked to generate a single random bit (see Section 4.8). If this bit is a 0, then the marker signal consists of the bits ‘1100’ in transmission order. If the bit is a 1, then the marker signal consists of the bits ‘0011’ in transmission order. This marker signal selection process shall be repeated if a sounding sequence of 96 bits is used and only if the second marker is not omitted.
Each marker signal shall overwrite four consecutive bits of the sounding sequence starting at a position determined by invoking the random number generation function hr1 (see Section 4.8.1). For the 32-bit sounding sequence, a single marker shall be used starting at bit number hr1(29) of the sequence (where the first bit is bit number 0). For the 96-bit sounding sequence, one or two markers shall be used. The first marker shall start at bit number hr1(64) and the second marker shall start at bit number hr1(75) + 67; if the starting bit position for the second marker exceeds 92, then the second marker shall be omitted.
See Section 4.8 for CS DRBG invocation ordering rules.
Figure 2.5 shows the construction of the sounding sequence with a single marker inserted. The sounding sequence is transmitted with the least significant bit first, and the most significant bit transmitted last.
2.5. Random sequence
The optional random sequence payload is a sequence of randomized bits. This random sequence is generated separately for each CS_SYNC transmitted. This bit sequence shall be generated using the output of the CS DRBG described in Section 4.8. The length of this bit sequence is identified by the RTT_Types selected during the CS configuration procedure described in [Vol 6] Part B, Section 5.1.25.
See Section 4.8 for CS DRBG invocation ordering rules.
The random sequence is constructed directly from the ordered bit output from the DRBG, with the first bit from the DRBG occupying the most significant bit of this field, which is the bit position equal to the length of the random sequence minus 1. The final bit from the DRBG occupies the least significant bit at position 0, as shown in Figure 2.6.
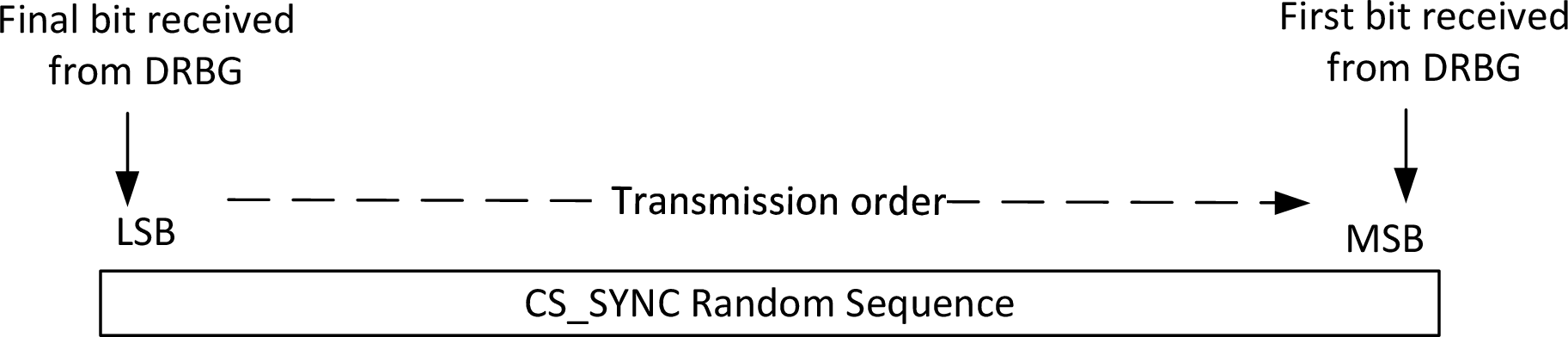
The random sequence is transmitted with the least significant bit first and the most significant bit transmitted last.
2.6. Channel Sounding extended packet formats
CS defines two additional packet formats.
A CS_SYNC followed by a CS tone is shown in Figure 2.7. The CS_SYNC has two mode-specific variations: a CS_SYNC_0_R, as described in Section 4.3.1, and a CS_SYNC_3_I, as described in Section 4.3.4.

A CS tone followed by a CS_SYNC is shown in Figure 2.8. In this case, the CS_SYNC occurrence is the CS_SYNC_3_R as described in Section 4.3.4.

In both cases, the guard time (T_GD) is 10 µs in duration, independent of the LE PHY being used. The transmitted signal during the guard time should be ignored by the receiver.
In both cases, the CS tone and CS_SYNC are transmitted on the same RF frequency and are subject to the rules of frequency and phase stability established in [Vol 6] Part A, Section 3.5. The duration of the two additional packet formats is variable and depends on various configuration factors, as described in Section 4.3.1 and Section 4.3.4.
3. Channel Sounding bit stream processing
3.1. Measuring RTT
Devices may use CS_SYNC exchanges to measure the propagation channel’s round-trip time (RTT).
Device A is the device that begins the RTT procedure with the transmission of the first packet in the RTT exchange. Device B is the device that receives the transmission from device A and then sends a response transmission back to device A.
Let ToDA represent the time of departure, measured at the antenna port, of the first packet transmitted in this exchange from device A. Also, let ToAA represent the time of arrival of the received packet, measured at the antenna port.
Similarly, let ToAB represent the time of arrival of the received packet from device A. Also, let ToDB represent the time of departure.
Consolidated, let ToXY represent the time of departure from device Y if X is replaced with D, or the time of arrival of arrival if X is replaced with A measured from device Y at its antenna port.
The value of ToXY is determined by optimizing the solution to the equation
where x̂Y(k,t) is the signal at the antenna port of Device Y during step k, after applying the reference down-conversion for a CS packet as defined in Section 3.1.1, and s(k,t) is the reference transmitted signal of the CS packet for step k as defined in Section 3.5.2. The value represents the symbol period. The value represents the start of the CS access address of the reference transmitted signal, where the preamble starts at t = 0. The value represents the end of the CS access address of the reference transmitted signal in the case of no random payload; alternatively, it represents the end of the random payload.
The RTT measurement obtained by Device A is obtained by using the difference of the values of ToAA − ToDA and ToDB − ToAB as expressed in the equation:
FFORX* is defined in [Vol 6]
Part A,
Section 3.5.1.
A single step for this exchange is shown in Figure 3.1.
 |
Devices should measure the ToD and ToA values as accurately and precisely as possible. Devices shall compensate for any known internal delays from the antenna to the actual measurement point for these values. Device A shall compensate for the effects of clock drift based on the FFO estimate of device B, relative to its own clock as described in [Vol 6] Part A, Section 3.5.1. Device A shall implement frequency-based timing compensation based on the equation above and using the value of FFORX*. Device B shall not attempt any related compensation for timing drift. Devices may choose to delay the start of their transmissions by up to one symbol period of the expected transmit point to increase the overall security of the RTT measurements.
Three variations of RTT timing estimates are defined in this section for the purpose of coordination between devices. A method for simultaneous extraction of a phase-based estimate along with an RTT timing estimate is also defined. Both device A and device B shall select the same method when performing both RTT timing and CS_SYNC phase-based estimates.
3.1.1. Reference receiver for round-trip time measurements
The reference down-conversion for the CS packet for step k = M + 1, …, M + K, is defined at the antenna of the device as
where x(t) is the signal at the antenna of device as defined in [Vol 6] Part A, Appendix B and LPF is a low-pass filter that removes the high frequency components. fE[k] represents the expected center frequency of the CS_SYNC packet as defined in [Vol 6] Part A, Section 3.5.2. x̂(t) is defined for all time t within step k.
3.1.2. ToD and ToA reporting accuracy
Let 2ToF represent the expected known two-way round-trip time of flight between device A and device B. In this section, the initiator is represented by device A and the reflector is represented by device B.
Denote (ToD − ToA)B[k] as the measurement value reported by Device B for step k.
Define the value of (ToD − ToA)′B[k]
where T_SY_CENTER_DELTA[k] is the value of T_SY_CENTER_DELTA for the mode used at step k as defined in Section 4.3.2 and Section 4.3.4. FFOE is the fractional frequency offset of the CS subevent as defined in [Vol 6] Part A, Section 3.5.2.
The error in Device B’s reported time measurement for step k, is defined as
where ToDB[k], ToAB[k] are the values measured as described in Section 3.1.
Similarly, denote (ToA − ToD)A[k] as the measurement value reported by Device A for step k that must include the correction for clock drift as described in Section 3.1.
Define the value of (ToA − ToD)′A[k] as
Let 2ToF represent the expected known two-way round-trip time of flight between device A and device B.
Device A’s RTT measurement error for step k, is defined as
where ToDA[k], ToAA[k] are the values measured by the tester as described in Section 3.1.
Let MeasurementValid[k] be equal to 1 if the CS Access Address quality indication value for the CS_SYNC received at step k is reported as 0, as described in Section 2.2.2. MeasuremetValid[k] is equal to 0 if the CS Access Address quality indication value is reported otherwise.
Within a single procedure i, with N steps of single packet exchanges, Device B’s procedure wise response time error is defined as
Similarly, Device A’s procedure wise RTT measurement error is given by
For Device B, the absolute bias is the absolute value of the mean of for Device B across procedures. The standard deviation of for Device B across procedures is denoted as . For Device A, the absolute bias is the absolute value of the mean of for Device A across procedures. The standard deviation of for Device A across procedures is denoted as .
Each device shall be characterized and the values of and shall meet one of two possible criteria at a receiver input level of -70 dBm:
for a minimum number of mode-1 and mode-3 CS_SYNC packet exchanges N per procedure, where N ≤ 255, or alternatively
for a minimum number of mode-1 and mode-3 CS_SYNC packet exchanges N per procedure, where N ≤ 255.
3.2. Timing estimate based on an Access Address
This section describes two methods for deriving ToA timing estimates based on the CS Access Address.
3.2.1. Timestamps using a native clock
Timestamping of the ToA may be done using the receiver’s native clock. The resolution provided by this method for a single sample is therefore proportional to the accuracy and clock rate of that receiver.
To improve the overall resolution of the measurement, measurements over several packets may be taken and averaged. Because the sampling clocks of a pair of devices are unrelated in phase, the distribution derived from several measurements is used to normalize the ToA value to a more precise average.
To improve the distribution of results, a transmitter may choose to transmit a CS_SYNC with an added fractional timing delay of up to one symbol period, which itself is pseudo-random with respect to the expected transmit point. The selection of the pseudo-random offset is left to the implementation.
3.2.2. Timing estimate based on a pseudo-noise bit sequence
RTT timing measurements may use a pseudo-noise sequence in a CS Access Address or payload, of sufficient length to obtain an indication of the timing error of the received signal with regard to the receiver’s local sampling clock. This timing error is the difference between the optimum sampling point and the actual sampling point, also known as the fractional timing component.
Several methods exist for extraction of this fractional timing component. One such method searches for the symbol correlation peak across all the symbols in the pseudo-noise sequence. Fractional timing extraction is not dependent on pseudo-random clock phase distribution between packet exchanges.
3.3. Fractional timing estimate based on a sounding sequence
Timing estimates may be derived from a modulated repeating [0 1] bit sequence. The modulation is either at the LE 1M PHY, the LE 2M PHY, or the LE 2M 2BT PHY. The periodicity of this sequence creates two distinct tones in the output spectrum, of which the periodic components are associated with the basic repetition of the two symbols. At the 1 Msym/s rate, this periodicity is at 2 µs. At the 2 Msym/s rate, it is at 1 µs.
Let
f represent the frequency of the complex sinusoid, and
α represent a common complex gain on these two signals.
The two complex sinusoid baseband signals are then denoted as
Now let
Ts represent the sampling period at the receiver,
n represent the number of samples of the respective complex sinusoids from a time t, and
M represent the integration period in units of full cycles of the complex sinusoids.
Then L, which represents the number of samples taken within that integration period, is denoted as
Denote the signal containing the modulated repeating [0 1] bit sequence as
Then the phase of the two complex sinusoids is measured through the following two correlations:
Because of the time quantization error and random sampling clock offset at the receiver, the estimated ToA timing measured at the receiver’s sampling clock rate is not the same as the actual ToA. Denote the coarse estimate of the start of the sounding sequence measured at the receiver’s antenna port as tsync. Using the two equations above, the fractional delay is calculated as:
The final estimate of the actual ToA is tsync + Δt, which is used for the ToA value in Section 3.1.
3.3.1. Phase-based PCT estimate based on a sounding sequence
The properties of the modulated repeating [0 1] bit sequence also allow for the extraction of distance estimates using phase-based calculations. Similar to RTT exchanges, the phase measurements consist of two exchanges and measurements, first in the direction from a device A to a receiving device B, then in the reverse direction. Exchanges over at least two channels are required to resolve the 2π ambiguity in the distance estimate.
Let
represent the RF initial phase of device A transmitting the signal,
represent the RF receive phase of the signal as seen at the receiving device B,
ѡlo represent the carrier frequency of that signal, and
ѡm represent the frequency of the modulated tones.
The complex representation of the modulated [0 1] signal at the transmitting device A is
Let
D represent the propagation distance, and
C represent the speed of light.
At the receiving device B, the representation of the receive signal is
After processing at the receiver, the equation above can be represented as
Applying the same correlations represented in Section 3.3, EQ X yields the following phase results for each of the two complex sinusoids:
At device B, to correct for phase change of the local oscillator while transmitting, the phase correction should be performed by complex multiplying both correlations by exp(j×phase_correction), where the phase correction is expressed in radians. The reference point for this definition is the local device’s antenna. The reference point for this definition is the local device’s antenna. SS_PCT results shall be consistent with the format for PCT results as described in Section 4.6. If a subevent contains PCT results, the same reference power level (RPL) should be used for the SS_PCT. Otherwise, the RPL shall be encoded as an 8-bit signed number. The RPL expressed in dBm shall correspond to the power of the sounding sequence sidelobe that produces a SS_PCT whose amplitude is 2048, obtained by integrating the received signal over the payload of the CS_SYNC packet at the expected sidelobe frequency. In all cases, a single RPL is used for all the SS_PCT values in a CS subevent.
The conversion between SS_PCT IQ values as unitless values to power in dBm can be expressed as denoted by EQ 4 in Section 4.6. In all cases the magnitude should be adjusted to give the power in the sounding sequence tone plus 6 dB.
These two equations can be further simplified, where ti is the same arbitrary time at which the correlations start, to
Then the phase-based rotation result from device A to device B is
Device B then reciprocates with a transmission of its own, and a similar result is obtained with device B as the transmitter and device A as the receiver. If both devices retain (or correct for) phase continuity in their local oscillators, then the phase-based rotation result from device B to device A is
When combined, these two results provide an estimated distance D between the two devices.
This estimate is compromised by the 2π ambiguity. To obtain an unambiguous range, the results from measurements over several frequencies, as defined in [Vol 2] Part A, Section 2, may be combined:
3.3.1.1. Reference receiver for phase-based ranging from a sounding sequence
Let the CS step at which a sounding sequence is exchanged occur at step index k as defined for CS tones in [Vol 6] Part A, Section 6.1. The reference down-conversion for the sounding sequence is then defined at the antenna of the device as
where x(t) is the signal at the antenna of a device used as defined in [Vol 6] Part A, Appendix B, and LPF is a low-pass filter that removes the high frequency components. fE[k] represents the center frequency of the CS_SYNC packet carrying the sounding sequence, as defined in [Vol 6] Part A, Section 3.5.2. x̂(t) is defined for all time t within step k.
Define the start time of the transmission of the sounding sequence from the vector signal generator as .
Denote the time of arrival of the CS Access Address of the transmission from the implementation under test as .
In the reference receiver, the following are also defined:
Ts represents the sampling period at the receiver.
Lss represents the length of the sounding sequence in terms of the number of symbols (see Section 2.4).
symbol_time is 1 µs for LE 1M and 0.5 µs for LE 2M and LE 2M 2BT.
represents the frequency of the complex exponential function used for correlations.
Then L, which represents one less than the number of samples taken within the integration period, is denoted as
3.3.1.2. Accuracy requirements
The observed average transmitted phase φtx(k,+f) and φtx(k,−f) for step k is measured through the following two correlations:
These results are then combined to give the observed average transmitted phase for step k, ΦTX[k]:
The observed average received phase and for step k is measured through the following two correlations:
These results are then combined for step k, according to the following equation:
The internal phase offset for step k is defined as
where principal( ) is defined in [Vol 6] Part A, Section 5.2.1, and SS_PCT1[k] and SS_PCT2[k] are the correlations defined in Section 3.3.1 for step k, provided by the IUT.
Denote θC,UW[k] as the phase-unwrapped version of θC[k].
Denote αfE,ord[k] + β as the solution to the linear regression of the set of points defined by (fE,ord[k], θC,UW[k]).
For any subevent where
An RTT Sounding Sequence of at least 32 bits is exchanged at least once for all CS channels,
the transmit signal received signal satisfies the conditions for frequency offset described in [Vol 6] Part A, Section 3.5.2, and
the receiver input level is -55dBm,
the solution to the linear regression shall satisfy
for 95% of subevents.
3.4. Fractional timing estimate based on a random sequence
Fractional RTT timing measurements based on a random sequence may use the same properties for the extraction of fractional timing components based on a pseudo-noise bit sequence as those described in Section 3.2.2. The symbol correlation peak derived from the individual symbols of an added random sequence bit field may be used to further refine the fractional timing extracted from the CS Access Address.
3.5. Attack detection requirements
This section describes a metric for reflecting the level of symbol attack detection, describes a reference signal construction, and provides reference attack signal definition. Reference attack signal definitions are used as a basis for detecting the presence of attack signals.
3.5.1. Normalized attack detector metric
The normalized attack detector metric (NADM) provides a measure of how much a received GFSK modulated packet signal differs from the expected packet signal as described in Section 3.5.2. A NADM value range indicates a progressively increased chance that an attacker is present. Refer to Table 3.1 for a description of these ranges.
Figure 3.2 shows the components of the overall attack detector system. The attack detector system uses a Controller-based NADM algorithm to determine a NADM value from each received packet in each CS device on both sides of the link. The NADM values are aggregated while an attack detector algorithm determines the threat level using the NADM values collected from one or more packet exchanges within a CS procedure. A user application can use the attack detector algorithm to determine its future actions.
The specifics of the user application and attack detector algorithm are beyond the scope of this specification.
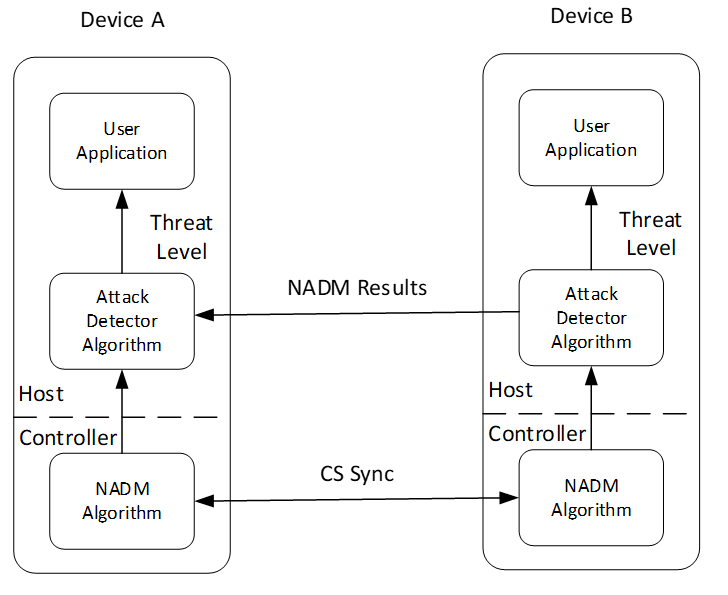 |
Figure 3.3 shows an example NADM system. In this example, a packet is received and its signal phase is extracted. This signal phase contains the relative phase information associated with the encoded data symbols from GFSK modulation. Because the data symbols for the received packet are known in advance, they can be modulated to construct a reference phase signal. A reference phase signal is described in Section 3.5.2. The received and reference signals should be similar. Differences in the phases of the two signals may be used to produce a raw attack detector metric. This raw metric may be combined with other information, such as the number of bit errors in the received signal, to produce the NADM.
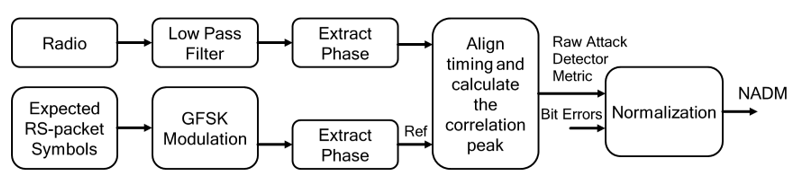
A raw detector metric for a CS_SYNC with sounding sequence or random sequence is described in Section 3.5.3.4.
The list of NADM values is shown in Table 3.1.
NADM | Attack Type |
|---|---|
0x00 | Attack extremely unlikely |
0x01 | Attack very unlikely |
0x02 | Attack unlikely |
0x03 | Attack is possible |
0x04 | Attack is likely |
0x05 | Attack very likely |
0x06 | Attack extremely likely |
0xFF | Unknown |
All other values | Reserved for future use |
Values starting from “Attack unlikely” through to “Attack extremely unlikely” indicate with increasing confidence the absence of an attacker. Values starting from “Attack is possible” through to “Attack extremely likely” indicate with increasing confidence the presence of an attacker. The implementation shall determine whether an attack is present or not present, and the selection of the level of confidence of that event. If a device is unable to determine a NADM value or does not support NADM processing, then it shall report a NADM value of Unknown (0xFF).
3.5.2. Reference signal modulated with BT=0.5, h=0.5 GFSK
Let B = [b0.. bN-1] be a binary sequence of N elements in the [0,1] space.
Let A = [a0.. aN-1] the symbol sequence of N elements corresponding to the binary sequence, following the mapping defined in [Vol 6] Part A, Section 3.1. Also, ai = 2bi − 1.
Let p(t) be a Gaussian-shaped pulse function of BT=0.5, for a normalized symbol period of 1, as defined by:
Where
And g(t) is the convolution of p(t) with a rectangle pulse of normalized duration 1, rect(t) = 1 when 0 < t < 1 and 0 otherwise.
Where the * operator represents the time convolution of the two signals.
Based on these definitions, the normalized reference phase is given by:
For a reference signal with symbol period TSym then the reference signal phase is defined as
and the reference signal is then
3.5.3. Early commit attacks with phase based detection
3.5.3.1. Sounding sequence attack signal definition
The format of the sounding sequence with marker insertion is described in Section 2.4. An early commit, late detect (ECLD) attack is a relevant MITM attack strategy due to the regular, repeating pattern of the sounding sequence. During an ECLD attack, the attacker receives the first device’s transmitted signal, and may regenerate the sounding sequence with a timing advance while searching for the randomized marker. The MITM attacker detects the marker while observing an unexpected bit transition (i.e., 0b1 to a 0b1, or 0b0 to a 0b0, instead of 0b1 to a 0b0, or 0b0 to a 0b1). The MITM may then change the phase trajectory to correct the rest of the symbol so the second device does not receive an incorrect symbol and the attack is not detected.
Table 3.2 shows the positions of the symbol(s) where an attacker-induced glitch might be detected given the symbol position of the marker start.
Symbol position of marker start | Symbol(s) with Glitch | |
|---|---|---|
Marker Sequence 0b0011 | Marker Sequence 0b1100 | |
k odd, original bit is 1 | k+1 and possibly k+2 | k and possibly k+1 |
k even, original bit is 0 | k and possibly k+1 | k+1 and possibly k+2 |
The following definitions are used to generate the attack signal:
Initialize the reference attack packet PA as the CS_SYNC packet without any markers in its sounding sequence. Define the oversampled discrete-time phase of the attack signal, ΦA[n], as the phase of the GFSK modulated version of PA. This is defined in terms of the reference signal defined in Section 3.5.2. where binary input sequence is PA. Then , where Tsym is the symbol period, and R is the oversampling rate within one symbol period.
The MITM attack signal is defined based on a detection delay of M samples of the original transmitted signal. The attacker determines a bit flip at the end of the detection delay and then applies a correction to follow its estimate of the original transmitted signal. The duration of this correction is denoted as the transition period. Table 3.3 shows this detection latency as well as other parameters (as explained below) that define this reference attack signal set.
Parameter
Value
Definition
R
≥ 16
Symbol oversampling rate
M
0.25R
Detection latency period
W
0.25R
Transition period
Table 3.3: Sounding Signal attacker signal configurationThe correction is a function of a Hanning window, that here is parameterized by its half window size width W:
Equation 0.
The reference attack signal is further defined as follows:
Denote position p, as the first bit in the packet that differs with the initial reference attack packet. If this bit is a 1, then the marker is 0b0011, otherwise it is 0b1100. For some bit positions there will be only one possible start position of marker. For example, if there is a bit flip in position 0 or 30 in the case of a single marker. If there is more than one possible start of the marker, then the attacker then makes a guess whether bit p is the first or second bit of the marker. This guess is independently distributed with equal probability. Denote the attacker's first guess of the marker start position as k1. If there is a valid second guess of the marker start position, denote this as k2.
Define P1 as the reference attack packet with the marker starting in position k1, and Φ1(n) as the signal obtained by GFSK modulating P1. Similarly, define P2 as the reference attack packet with the marker starting in position k2, and Φ2(n) as the signal obtained by GFSK modulating P2.
Modify the phase trajectory of the reference attack signal ΦA(n) at samples from symbol starting at n = R × p + 1.
Segment 1: during the first M samples (detection latency period), the current reference attack signal is sent:
Equation 0.Segment 2: during the next W samples (transition period), a (half) Hanning windowed phase transition is applied from ΦA(R × p + M + 1) to the first guess Φ1(R × p + (M + W)):
Equation 0.Equation 0.Segment 3: in this segment, the phase trajectory follows the first guess:
Equation 0.The reference attack packet becomes P1 i.e. PA ← P1.
In the case that the attacker’s first guess is wrong, then the attacker observes a bit flip at p′ = p + 1. The attacker then modifies the phase trajectory of the attack signal ΦA(n) to produce a second glitch. Define the phase trajectory as follows:
Segment 1: during the first M samples (detection latency period), the current reference attack signal is sent:
Equation 0.Segment 2: during the next W samples (transition period), a (half) Hanning windowed phase transition is applied from ΦA(R × p′ + M + 1) to the correct phase Φ2(R × p′ + (M + W)):
Equation 0.Equation 0.Segment 3: in this segment, the phase trajectory follows the second guess:
Equation 0.The reference attack packet becomes P2 i.e. PA ← P2.
If the marker is the first marker in the packet, and there exists a second marker in the packet, then return to step 1. Otherwise, the reference attack signal is ΦA(n).
3.5.3.2. Random sequence attack signal definition
The phase of an attacker signal is the sum of the ideal reference signal with symbol period Tsym as defined in Section 3.5.2 and an adjustment term ψ(t):
The adjustment term approximates the behavior of an MITM attack to make the sequence appear earlier than the original signal. This adjustment is achieved by applying a phase transition using a Gaussian mono-pulse early within the symbol period. The sign of the pulse acting over symbol n is determined by the symbol value an.
For each encoded symbol a pulse is added to ψ(t) centered at , where p is a time adjustment that significantly defines the attacker’s desired distance offset.
In this context, a Gaussian mono-pulse is defined as minus the derivative of a Gaussian pulse. The width of the pulse is roughly Tsym÷K, where K is the pulse sharpness factor. The magnitude M, time adjustment p, and sharpness factor K are used to manipulate the timing of Φa(t) compared to .
ψ(t) is defined as
where is the symbol sequence as defined in Section 3.5.2.
Table 3.4 shows the parameters from EQ 5 that define a Reference attack signal set for LE 1M and LE 2M.
Parameter | Definition | Value LE1M | Value LE 2M | Value LE 2M 2BT |
|---|---|---|---|---|
K | Pulse sharpness factor | 12 | 12 | 12 |
M | Pulse sharpness factor | 3 | 3 | 3 |
p | Pulse time adjustment factor These values of p equate to approximately 3 meters of distance decrease. | -0.56 | -0.61 | -0.62 |
T sym | Symbol period in microseconds | 1.0 | 0.5 | 0.5 |
3.5.3.3. Raw attack detector metric based on a sounding sequence or a random sequence
A raw attack detector estimate may be derived from a modulated random sequence if this sequence is known between a transmitting and receiving set of devices. A preconstructed reference model based on this sequence is used as a basis of comparison for detecting symbol manipulation.
The modulation of the signal for which an attack detection estimate is generated is either at the 1 Msym/s rate or at the 2 Msym/s rate.
Let
f represent the frequency of the modulated bits.
Ts represent the sampling period at the receiver.
M represent the integration period in units of symbol full cycles.
The integration period for an RTT with sounding sequence is the span of symbols with the possibility of detectable glitches when manipulation is present, as defined in Section 2.4. The integration period for RTT with random sequence is the span of the entire random sequence, as defined in Section 2.5.
Let , which represents the number of samples within each full symbol, be denoted as
And L, which represents the number of samples within the full integration period, is denoted as
Denote the measured signal containing the random sequence as
Similarly, denote the reference signal of that same random sequence as
Then the instantaneous phase of the measured signal and the reference signal, respectively, are
The phase of the measured signal is then compared to the reference signal to calculate the quality factor. Ambiguity exists between the start instants of the two signals, because the data points of the two signals are collected separately and because of quantization error at the receiver.
Two reference methods for deriving a raw attack detector metric are described.
3.5.3.3.1. Raw attack detector metric based on normalized cross correlation
Normalized cross-correlation may be used to compare a measured signal to a reference signal. In the following description, the mean phase of the reference signal is shifted over a full symbol worth of sample offsets. Then each reference mean phase value is compared with the mean phase of the measured signal.
Let L′, which represents the maximum number of samples to process within an integration period that is one full sample less than the full integration period, be denoted as
Denote the mean of the phase of the measured signal as
Similarly, denote the mean of the phase of the reference signal over a full symbol worth of sample offsets as
Cross-correlation is then calculated over the relative phase of the two signals, with a lag span of a full symbol cycle to compensate for receiver quantization error.
The autocorrelation result of the two signals is then
From this result, a raw attack detector metric can be derived.
3.5.3.3.2. Raw attack detector metric based on phase minimum square error
Phase minimum square error is an alternate method for comparing a measured signal to a reference signal. In contrast to the description in Section 3.5.3.3.1, the mean phase of the collected signal is shifted over a full symbol worth of sample offsets starting ½ symbol before the nominal start point. Then each measured mean phase value is compared with the mean phase of the reference signal.
Let l′ represent the number of samples within ½ of a full symbol, and be denoted as
Denote the mean of the phase of the measured signal over sample offsets z in the range −l′ + 1 to l′, relative to the nominal start and end of the target symbol(s) used in the comparison, as
Similarly, denote the mean of the phase of the reference signal as
The phase square error is then calculated as
The minimum phase mean square error is then
From this result, a raw attack detector metric can be derived.
3.5.3.4. Phase-based attack detection requirements for RTT with sounding sequence and random sequence packets
This section describes how the RTT with sounding sequence or RTT with random sequence and the normalized attack detector metric (NADM) shall be tested. CS mode-1 and CS mode-3 steps, described in Section 4.3, carry the packet contents.
This test requires a tester CS device that can transmit either a normal signal or an attacker signal during mode‑1 and mode‑3 CS steps. The normal signal is the transmitted signal after either the sounding sequence or random sequence portion has been modulated using normal GFSK. The attacker signal is the normal signal, but with its phase adjusted to approximate a signal from an MITM attack. The attacker signal for RTT with sounding sequence is defined in Section 3.5.3.1. The attacker signal for RTT with random sequence is defined in Section 3.5.3.2.
The tester device shall generate a reference signal of -67 dBm power together with a Gaussian Noise Floor of -152 dBm/Hz for the LE1M PHY. The tester device shall generate a reference signal of -67 dBm power together with a Gaussian Noise Floor of -155 dBm/Hz for the LE2M PHY.
The tester device acts as an initiator to start a CS procedure with the IUT. Each test comprises one or more CS procedures executing the total CS subevent count specified in Table 3.5 and Table 3.6. Each CS subevent comprises a normal mode-0 CS step, followed by a single mode-1 CS step or a mode-3 CS step with specified sounding and random sequence lengths.
For each CS step, the tester device makes a random decision to transmit either a normal signal or an attacker signal. The tester CS device records these random decisions over the whole CS procedure. These random decision sequences are later compared with the resulting NADM values from the IUT.
Table 3.5 and Table 3.6 define multiple mandatory tests that depend on the supported capabilities of the IUT. The tests are designed to verify the minimum performance for a NADM value. RTT packets are used in mode-1 and mode-3 and are both tested. LE 1M, LE 2M, and LE 2M 2BT are also tested. For RTT with sounding sequence, the attacker signal is designed to exhibit abnormal phase glitch behavior around the associated marker bits. For RTT with random sequence, the attacker signal is designed to appear D meters (see Table 3.6) earlier than the normal signal.
Test | LE PHY | RTT Step Type | Sounding Sequence Length (bits) | Number of Subevents | Expected min SNR in Reflector-Under-Test / dB | Detection Latency | Transition Period |
|---|---|---|---|---|---|---|---|
1 | LE 1M | Mode-1 | 32 | 100 | 25 | ¼ symbol | ¼ symbol |
2 | LE 1M | Mode-3 | 32 | 100 | 25 | ¼ symbol | ¼ symbol |
3 | LE 2M | Mode-1 | 32 | 100 | 25 | ¼ symbol | ¼ symbol |
4 | LE 2M | Mode-3 | 32 | 100 | 25 | ¼ symbol | ¼ symbol |
5 | LE 2M 2BT | Mode-1 | 32 | 100 | 25 | ¼ symbol | ¼ symbol |
6 | LE 2M 2BT | Mode-3 | 32 | 100 | 25 | ¼ symbol | ¼ symbol |
Test | LE PHY | RTT Step Type | Random Sequence Length (bits) | Number of Subevents | Expected min SNR in Reflector-Under-Test / dB | Manipulated Distance D for Attacker (meters) |
|---|---|---|---|---|---|---|
1 | LE 1M | Mode-1 | 32 | 100 | 25 | -3 |
2 | LE 1M | Mode-3 | 32 | 100 | 25 | -3 |
3 | LE 2M | Mode-1 | 32 | 100 | 25 | -3 |
4 | LE 2M | Mode-3 | 32 | 100 | 25 | -3 |
5 | LE 2M 2BT | Mode-1 | 32 | 100 | 25 | -3 |
6 | LE 2M 2BT | Mode-3 | 32 | 100 | 25 | -3 |
After each test is complete, the tester device shall compare the NADM values from each RTT packet against the random attack decision sequence it recorded earlier. For each test, 90% of the NADM values shall correctly identify the presence or absence of an attacker as defined in Section 3.5.1.
4. Channel Sounding interface protocol
4.1. Channel selection Algorithm #3
The algorithms described in this section support Channel Selection for each CS step within a CS procedure. A CS step involves the execution of one of four CS modes, described in Section 4.3. The algorithms described here generate a set of channel indices on which the mode exchanges take place.
Two sets of channel indices are generated. The first sequence defines the hopping pattern used by mode-0 CS steps. The second sequence defines the hop pattern used by non-mode-0 CS steps. Two separate algorithms are defined for the latter sequence.
Each sequence is further filtered by the channel index filter bit map CSFilteredChM, which is described in [Vol 6] Part B, Section 5.1.28. In that bit map, a bit set to 1 indicates that the channel represented by that bit shall be included in the resulting hop set. A bit set to 0 indicates that the channel represented by that bit shall not be included in the resulting hop set. Prohibited channel indices shall be immediately excluded from the resulting hop set (see [Vol 2] Part A, Section 2).
Each resulting channel index array shall be used starting from index 0 in ascending order whenever a CS step (either mode-0 or non-mode-0) is executed. Each entry in the resulting channel index array shall only be used once unless otherwise specified in this specification. After it is exhausted, this array shall be regenerated at the CS step where a new channel index is needed.
4.1.1. Conventions
The following procedural conventions are used in this description of Channel Selection Algorithm #3.
Function | Meaning |
|---|---|
length_of() | Returns the populated length of an unsigned integer array |
4.1.2. Channel index shuffling function cr1
When deriving the channel index selection within a CS procedure, the CS DRBG is invoked to shuffle the list of available channels. The channel index shuffling function cr1 is defined for this purpose. The inputs to cr1 are a one-dimensional unsigned integer array, ChannelArray, that lists all available channel indices, and the length of that array, nChannels.
The following are values returned from cr1:
ShuffledChannelArray, a one-dimensional unsigned integer array of length nChannels
The following temporary values are used:
i, j are unsigned integers
The input/output format of cr1 is as follows:
ShuffledChannelArray = cr1( nChannels, ChannelArray )
cr1 processing is as follows:
for i = 0 to nChannels – 1 do j = random integer such that 0 <= j <= i if i != j ShuffledChannelArray[ i ] = ShuffledChannelArray[ j ] ShuffledChannelArray[ j ] = ChannelArray[ i ]
The random integer j noted above shall be seeded using the random number generation function hr1 (see Section 4.8.1). The random integer j shall be computed using the increasing index i from above as follows:
hr( i + 1 )
4.1.3. Channel selection Algorithm #3a for mode‑0 steps
Channel Selection Algorithm #3a is used to generate a randomized channel map with uniform distribution for mode‑0 CS steps.
The number of times that the mode-0 channel list is regenerated in a CS procedure depends on several factors, including:
The size of the list of included filtered channels as indicated by the filter channel bit map CSFilteredChM
The number of mode-0 steps included in a CS subevent
The number of CS subevents within a CS procedure
The run-time construction of CS subevents, whose content may vary from subevent to subevent as described in Section 4.4
The randomized channel map is created by first converting the filtered channel bit map to a one-dimensional unsigned integer array of channel indices that shall include only the indices of the CSFilteredChM marked as included, as described in Section 4.1. This intermediate array is called the filteredChannelArray. The filteredChannelArray is used to create a shuffled channel list in an array of the same size, the Mode0ShuffledChannelArray. The Mode0ShuffledChannelArray is generated using the channel index shuffling function cr1 (see Section 4.1.2) as follows:
Mode0ShuffledChannelArray = cr1( length_of( filteredChannelArray ), filteredChannelArray )
4.1.4. Channel index selection for non-mode‑0 steps
Channel Selection Algorithms #3b and #3c support channel selection for each non-mode‑0 CS step within a CS procedure. Only one of the two algorithms shall be used within a single CS procedure.
The number of times the non-mode-0 channel list shall be regenerated in a CS procedure depends on several factors, including:
The size of the list of included filtered channels as indicated by the filter channel bit map CSFilteredChM
The number of times the filtered channel map is repeated in a procedure for non-mode-0 steps, as defined by CSNumRepetitions (see [Vol 6] Part B, Section 5.1.26)
The run-time construction of CS subevents whose content may vary from subevent to subevent, as described in Section 4.4
4.1.4.1. Channel Selection Algorithm #3b
Channel Selection Algorithm #3b is used to generate a randomized channel map with uniform distribution for non-mode‑0 CS steps.
The filtered channel bit map is first converted to a one-dimensional unsigned integer array of channel indices that shall include only the indices of the CSFilteredChM marked as included, as described in Section 4.1. This intermediate array is called the filteredChannelArray. The resulting shuffled channel list is held in an array of the same size and is known as NonMode0ShuffledChannelArray. To generate this array, the channel index shuffling function cr1 (see Section 4.1.2) shall be invoked as follows:
NonMode0ShuffledChannelArray = cr1( length_of( filteredChannelArray ), filteredChannelArray )
4.1.4.2. Channel Selection Algorithm #3c
Channel Selection Algorithm #3c integrates rising and falling ramps into the resulting channel map for non-mode‑0 CS steps. These ramps are useful for estimating timing drift and object motion correction. The ramps have the shape of either a hat or an X pattern. In a hat shape, a rising ramp is directly followed by a falling ramp. In an X pattern, rising and falling ramps are interleaved. These shapes are incorporated into a shuffled channel map so that they appear random, preserving equal channel distribution qualities.
A block diagram of the overall algorithm is shown in Figure 4.1. Each process block, as well as inputs and outputs, are described in subsequent sections.

4.1.4.2.1. Inputs and basic components
Channel Selection Algorithm #3c has the following inputs:
CSShapeSelection – indicates the selection of either the hat shape or the X pattern.
CSChannelJump – indicates the number of channels skipped over when rendering the selected shape, based on the CS channel index values described in Section 1.
CSNumRepetitions – indicates the number of times Channel Selection Algorithm #3c is invoked. This number is the same as the number of times the filtered channel bit map is repeated within that CS procedure.
Table 4.2 shows additional algorithm-related parameters. The value selected for CSChannelJump determines which row in Table 4.2 shall be used in Channel Selection Algorithm #3c.
CSChannelJump | seq1StartCh | seq2StartCh | maxRepsAllowed | saltRate |
|---|---|---|---|---|
2 | 1 | 76 | 1 | 2 |
3 | 77 | 0 | 1 | 2 |
4 | 78 | 0 | 2 | 2 |
5 | 78 | 0 | 2 | 2 |
6 | 76 | 1 | 3 | 2 |
7 | 74 | 1 | 3 | 2 |
8 | 76 | 0 | 3 | 2 |
The values of seq1StartCh and seq2StartCh denote the starting channel index used to construct the two ramps of the selected shape indicated by CSShapeSelection. These parameters refer to the CS channel index values described in Section 1.
maxRepsAllowed is the upper limit of the CSNumRepetitions parameter. The value of CSNumRepetitions shall be greater than or equal to 1 and less than or equal to maxRepsAllowed.
saltRate is the rate at which alternate hop channels are inserted into the constructed hopping pattern. These alternate hop channels shall not include the channels used in the shape construction selected by the CSChannelShape parameter. These alternate channels are mixed into the hopping pattern for uniform channel distribution containing the valid set of CS physical channels. This alternate set of channels is referred to as salt channels.
Multiple instances of the non-mode-0 channel map, and therefore multiple iterations of the Channel Selection Algorithm #3c procedure, are required if CSNumRepetitions is greater than 1. The integer value nShapeIteration shall be maintained for each active CS procedure. nShapeIteration shall be initialized to 0 for the first iteration of this algorithm within that CS procedure and shall be incremented by one before the next iteration of the Channel Selection Algorithm #3c procedure.
4.1.4.2.2. Shape generation
Each invocation of Channel Selection Algorithm #3c begins with the identification of the channels used to hold the shape selected by the CSShapeSelection parameter. The function of the process block GenShapeSequence shown in Figure 4.1 is described in this section.
The shape generation function returns the following:
ShapeChSeq – a one-dimensional unsigned integer array that holds the channel set constructed to form the selected shape
For the purpose of long-term uniform channel distribution, the starting position of the channel sequence that constructs the selected shape is shifted by a value from 0 to CSChannelJump -1 channel indices. The random number generation function hr1 (see Section 4.8.1) is invoked to produce the random startJitter value. If this is the first instance of the non-mode‑0 channel map generation procedure with a CS procedure, which shall be the case when nShapeIteration is equal to 0, then the startJitter value is produced as follows:
startJitter = hr1( CSChannelJump )
Otherwise, the value of startJitter shall be held constant for the remaining duration of the CS procedure.
The ShapeChSeq content is then generated as follows:
The shape ramp offset values, s1Ch and s2Ch, are calculated as follows:
offset = (nShapeIteration + startJitter) mod CSChannelJump
s1Ch = seq1StartCh + offset
s2Ch = seq2StartCh + offset
Each shape ramp is computed starting from the channels identified by s1Ch and s2Ch. Channels are appended through the valid channel map range defined by the CS channel index values described in Section 1. Each computed channel value is appended to the ShapeChSeq array in turn.
If CSShapeSelection is the X pattern, the channels offset from s1Ch and s2Ch are interleaved when appended to ShapeChSeq starting with s1Ch. If seq1StartCh is less than seq2StartCh, an increment value inc is set to CSChannelJump. If seq1StartCh is greater than or equal to seq2StartCh, inc is set to -1xCSChannelJump. Starting with s1Ch, s1Ch and s2Ch are alternately recomputed as follows and appended to the ShapeChSeq array. For each of the two individual computations, the first few sequential values may fall outside of the channel map range (see Section 1) and if so, those individual values shall not be appended to the ShapeChSeq array. Thereafter, while each newly computed value still remains within the valid channel map range, the values are appended similarly. If one of the two values then falls out of the valid channel map range, then the other value continues to be processed and appended to the ShapeChSeq array until it also falls out of the valid channel map range.
s1Ch = s1Ch + inc
s2Ch = s2Ch – inc
If CSShapeSelection is the hat pattern, the entire rising ramp is appended to ShapeChSeq before the falling ramp by determining which ramp s1Ch and s2Ch represent, using the following procedure. In the procedure, risingCh is the set of channel indices for the rising ramp and fallingCh is the set of channel indices for the falling ramp.
If s1Ch is less than s2Ch, then risingCh = s1Ch and fallingCh = s2Ch. If s1Ch is greater than or equal to s2Ch, risingCh = s2Ch and fallingCh = s1Ch.
The increment value of CSChannelJump is used.
The values based on risingCh are computed first. The first few sequential values may fall outside of the valid channel map range (see Section 1) and if so, shall not be appended to the ShapeChSeq array. Thereafter, the next computed values are appended to the ShapeChSeq array while they remain within the valid channel map range.
risingCh = risingCh + CSChannelJump
Thereafter, the values based on fallingCh are computed. The first few sequential values may fall outside of the valid channel map range (see Section 1) and if so, shall not be appended to the ShapeChSeq array. Thereafter, the next computed values are appended to the ShapeChSeq array while they remain within the valid channel map range.
fallingCh = fallingCh − CSChannelJump
4.1.4.2.3. Salt generation
Salt channels are used to generate a uniform channel distribution in the valid set of CS physical channels, as defined in Section 1. The function of the process block GenSalt, shown in Figure 4.1, is described in this section.
The salt channel generation function returns the following:
FirstAndEndSaltChSeq – a one-dimensional unsigned integer array holding an intermediate salt channel list
MiddleSaltChSeq – another one-dimensional unsigned integer array holding a second intermediate salt channel list
Salt channels are channels that are not part of the shape generation list ShapeChSeq described in Section 4.1.4.2.2 but are still valid CS channel index values as described in Section 1. The list of available salt channels for a specific hop channel generation procedure is derived by direct comparison against the shape generation channel list ShapeChSeq.
The list of candidate salt channels is populated in a one-dimensional unsigned integer array called unusedChSeq, which is first initialized as an empty list. Starting from channel index 0 in ascending order, each valid CS channel index as described in Section 1 is compared to the ShapeChSeq array. If a channel index is not present, then that channel index is appended to the unusedChSeq list.
The valid CS physical channel range is then divided into four quadrants which approximately surround the channel shape held in the ShapeChSeq. This grouping is shown in Figure 4.2. In the figure, the vertical lines show stepwise sequence boundaries, and the horizontal lines show channel segmentation boundaries for the entire valid CS physical channel range. The boxes denote a delineation of the salt channel set. The boxes labeled First and End contain the same set of channels, corresponding to the first and end quadrants of the shape. Approximately 50% of the valid CS physical channel range is divided between the First and the End, and the remaining physical channel range is contained within the Middle boxes.
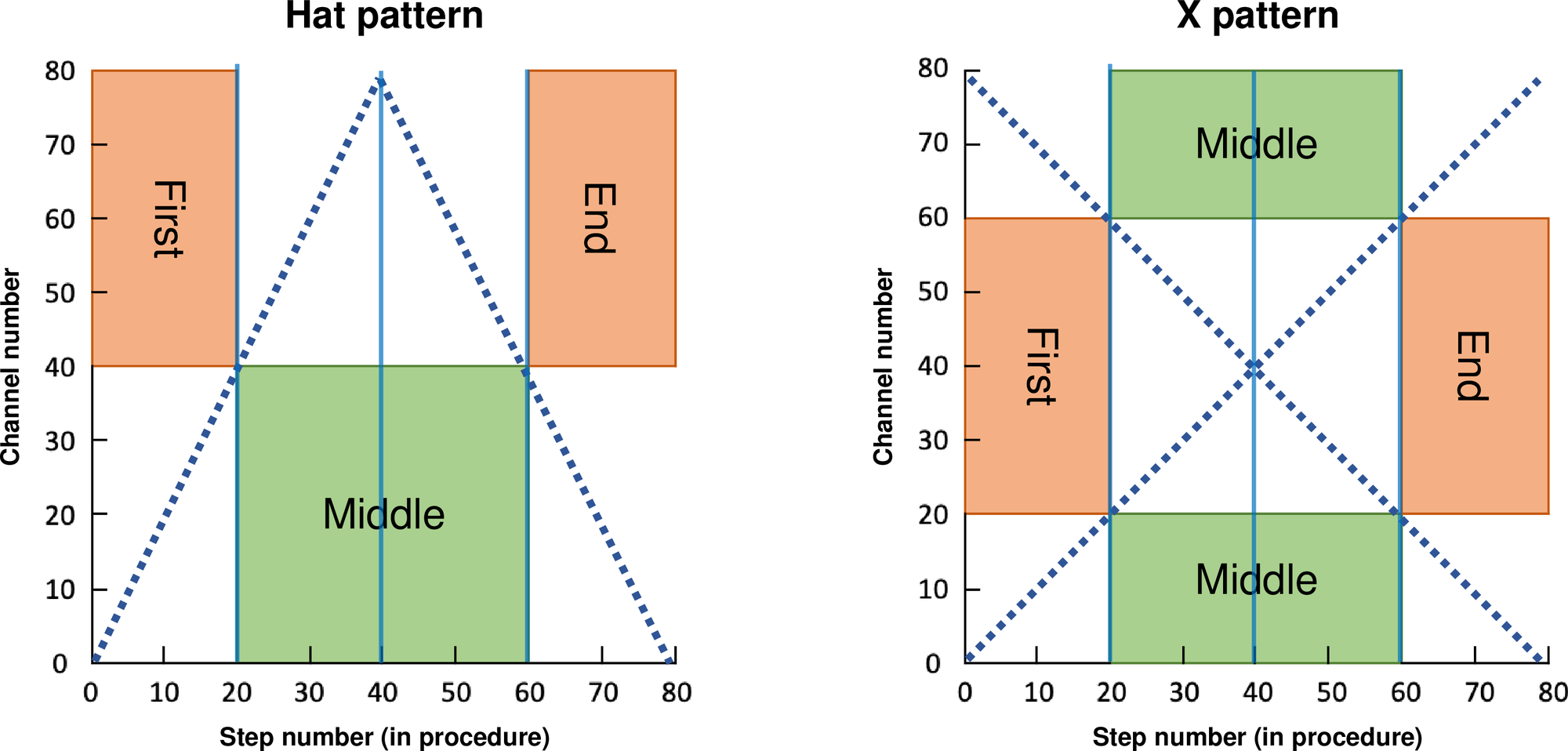
Four unsigned integer arrays holding intermediate sequences divide the valid CS physical channel range into four approximately equal sized regions:
chQ1All = [0, 19] chQ2All = [20, 39] chQ3All = [40, 59] chQ4All = [60, 78]
From the arrays above, a second set of intermediate sequences are constructed and held in another set of four unsigned integer arrays initialized as empty lists: chQ1Unused, chQ2Unused, chQ3Unused, and chQ4Unused. The content of each of these four channel sets is compared to the previous unusedChSeq in search of common channels. Each channel in chQ1All is compared with the content of unusedChSeq. If a channel in chQ1All appears in unusedChSeq, it is appended to the chQ1Unused array. This process is repeated to construct the content of chQ2Unused, chQ3Unused, and chQ4Unused.
From the content generated for chQ1Unused, chQ2Unused, chQ3Unused, and chQ4Unused, a third set of intermediate sequences is constructed and held in another set of four unsigned integer arrays: firstAndEndUnusedChSeq, firstAndEndAllChSeq, middleUnusedChSeq, and middleAllChSeq. The construction of these sequences depends on the shape selected with CSShapeSelection.
If CSShapeSelection is the X pattern, then
firstAndEndAllChSeq is constructed by concatenating chQ3All to the end of chQ2All.
middleAllChSeq is constructed by concatenating chQ4All to the end of chQ1All.
firstAndEndUnusedChSeq is constructed by concatenating chQ3Unused to the end of chQ2Unused.
middleUnusedChSeq is constructed by concatenating chQ4Unused to the end of chQ1Unused.
If CSShapeSelection is the hat pattern, then
firstAndEndAllChSeq is constructed by concatenating chQ4All to the end of chQ3All.
middleAllChSeq is constructed by concatenating chQ2All to the end of chQ1All.
firstAndEndUnusedChSeq is constructed by concatenating chQ4Unused to the end of chQ3Unused.
middleUnusedChSeq is constructed by concatenating chQ2Unused to the end of chQ1Unused.
The channel index shuffle function cr1 (see Section 4.1.2) shall then be invoked on each of the above four intermediate channel sequences as follows:
firstAndEndAllChSeq = cr1( firstAndEndAllChSeq, length_of( firstAndEndAllChSeq )) middleAllChSeq = cr1( middleAllChSeq, length_of( middleAllChSeq)) firstAndEndUnusedChSeq = cr1( firstAndEndUsusedChSeq, length_of( firstAndEndUsusedChSeq)) middleUnusedChSeq = cr1( middleUnusedChSeq, length_of( middleUnusedChSeq))
FirstAndEndSaltChSeq is then constructed by concatenating firstAndEndAllChSeq to the end of firstAndEndUnusedChSeq. MiddleSaltChSeq is constructed by concatenating middleAllChSeq to the end of middleUnusedChSeq.
4.1.4.2.4. Shape and salt channel mixing
After salt channels are generated, shape channels are mixed with salt channels. The function process block SaltChannelInsertion shown in Figure 4.1 is described in this section.
The following is returned from the salt channel insertion function:
SaltedChSeq – a one-dimensional unsigned integer array containing the salted shape channel sequence
SaltedChSeq is first initialized as an empty list.
If this is the first instance of non-mode-0 channel map generation procedure within a CS procedure, which shall be the case when nShapeIteration is equal to 0, then a random set of between 0 and CS3C_N_INITIAL_SALT salt channels shall be appended to SaltedChSeq as follows:
CS3C_N_INITIAL_SALT shall be equal to 9.
The random number generation function hr1 (see Section 4.8.1) is invoked to generate the random nInitialSalt value as follows:
nInitialSalt = hr1( CS3C_N_INITIAL_SALT + 1 )
Beginning from element 0, nInitialSalt channels are appended to SaltedChSeq, starting with the FirstAndEndSaltChSeq array and alternating between the FirstAndEndSaltChSeq array and the MiddleSaltChSeq array.
Shape channels and salt channels are then appended in a mixing fashion. Channels from arrays ShapeChSeq (starting from element 0), FirstAndEndSaltChSeq, and MiddleSaltChSeq are selected and appended to the SaltedChSeq array. Channels from the originating arrays shall be consumed in ascending order and never reused. Previously consumed channels from the FirstAndEndSaltChSeq and MiddleSaltChSeq arrays are also not reused. Channels from these arrays are consumed starting with the next available entry. In the procedure below, i and j are temporary variables.
For i = 0 to length_of( ShapeChSeq ) - 1 do if ( i mod saltRate ) == 0 Append a salt step to SaltedChSeq as described below. Append the next entry from ShapeChSeq to SaltedChSeq.
In the procedure above, when a salt step is appended to the SaltedChSeq, the following procedure shall be used.
j = ( ShapeChSeq[i] ÷ 20 ) + 1 if CSShapeSelection is the X pattern if ( j == 1 ) or ( j == 4 ) Append the next entry from FirstAndEndSaltChSeq to SaltedChSeq else Append the next entry from MiddleSaltChSeq to SaltedChSeq else if CSShapeSelection is the hat pattern if ( j == 1 ) or ( j == 2 ) Append the next entry from FirstAndEndSaltChSeq to SaltedChSeq else Append the next entry from MiddleSaltChSeq to SaltedChSeq
If this procedure is the last instance of the non-mode-0 channel map generation procedure within the CS procedure, which shall be the case when nShapeIteration is equal to CSNumRepetitions-1, then a random set of between 0 to CS3C_N_FINAL_SALT salt channels is appended to SaltedChSeq as follows:
CS3C_N_FINAL_SALT shall be equal to 4.
The random number generation function hr1 (see Section 4.8.1) is invoked to generate a random nFinalSalt value as follows:
nFinalSalt = hr1( CS3C_N_FINAL_SALT + 1 )
nFinalSalt channels are appended to SaltedChSeq, starting first from the next available FirstAndEndSaltChSeq array and alternating between the next available FirstAndEndSaltChSeq array and the next available MiddleSaltChSeq array.
If more channels from FirstAndEndSaltChSeq than from MiddleSaltChSeq were appended to the SaltedChSeq, then the deficit amount of the next available entries from MiddleSaltChSeq are appended to the end of SaltedChSeq. Alternatively, if more channels from MiddleSaltChSeq than from FirstAndEndSaltChSeq were appended to the SaltedChSeq, then the deficit amount of the next available entries from FirstAndEndSaltChSeq are appended to the end of SaltedChSeq.
Any remaining entries from the FirstAndEndSaltChSeq and MiddleSaltChSeq shall be discarded.
4.1.4.2.5. Filtering and shuffling
After the SaltedChSeq array is generated, it is then filtered through the filter channel bit map CSFilteredChM described in [Vol 6] Part B, Section 5.1.28. The resulting filtered channel set is then shuffled in a block-based fashion. The function process block FilterAndShuffle shown in Figure 4.1 is described in this section.
The following is returned from the filtering and shuffling function. It is also the final output of Channel Selection Algorithm #3c:
NonMode0ShuffledChannelArray – a one dimensional unsigned integer array containing the non-mode‑0 channel index array
If this is the first instance of the non-mode-0 channel map generation procedure with a CS procedure, which shall be the case when nShapeIteration is equal to 0, then NonMode0ShuffledChannelArray is initialized as an empty list. Otherwise, the prior content of NonMode0ShuffledChannelArray is appended to by the procedure described in this section.
filteredSaltedChSeq is an intermediate unsigned integer array that holds the filtered channel content of the SaltedChSeq array. filteredSaltedChSeq is initialized as an empty list.
The content of the SaltedChSeq is filtered using the content of the CSFilteredChM bit map. Each bit position of the CSFilteredChM starting from bit 0, represents a valid CS channel index as described in Section 1. If a bit is set to 0, then that channel index is filtered out. Otherwise, if a bit is set to 1, then that channel index is allowed for use within a CS procedure. Starting from the first element, the content of the SaltedChSeq array is compared with the content of the CSFilteredChM bit map. Channels that are not filtered out are then appended to the filtered sequence filteredSaltedChSeq in order. Channels that are filtered out are discarded.
The content remaining in filteredSaltedChSeq is then shuffled in smaller block quantities. The size of each block is computed as follows.
Therefore, the number of blocks contained in the filteredSaltedChSeq array can be derived as follows.
NonMode0ShuffledChannelArray is then constructed by shuffling filteredSaltedChSeq in blocks of nStepsInBlock channels. This starts from the beginning of the filteredSaltedChSeq and progresses through the entire array content. The channel index shuffling function cr1 (see Section 4.1.2) shall be invoked as follows. Here i is a temporary unsigned integer and tempBlockSeq is a temporary unsigned integer array. filteredSaltedChSeq is referenced starting from the first element at array position 0.
For i = 0 to nBlocksToShuffle-1 delete all content from tempBlockSeq if i < nBlocksToShuffle-1 // not the last block in filteredsaltedChSeq Copy elements ( i x nStepsInBlock ) to ((( i + 1 ) x nStepsInBlock ) – 1 ) of filteredChSeq to tempBlockSeq else Copy remaining elements filteredChSeq to tempBlockSeq tempBlockSeq = cr1( tempBlockSeq, length_of( tempBlockSeq )) Append tempBlockSeq to NonMode0ShuffledChannelArray
4.2. Channel Sounding channel indices
Channel Selection Algorithm #3 shall be used to define the frequency hop pattern for all CS steps within a CS procedure. This hop pattern is seeded by the CSChM and the CSNumRepetitions parameters of the CS configuration selected for that procedure (see [Vol 6] Part B, Section 5.1.26) as well as the running channel map update (see [Vol 6] Part B, Section 5.1.28). The maximum number of non-mode‑0 steps included in a CS procedure shall be bounded by the number of used channels in the CSFilteredChM channel map (see [Vol 6] Part B, Section 5.1.28) multiplied by the CSNumRepetitions parameter, plus any salted channel insertions as described in Section 4.1.4.2 and any steps that reuse channels as described in this section and in Section 4.4.
A CS procedure is considered complete and closed when at least one of the following conditions occurs.
The execution of the next CS step in its entirety would cause the extent of the CS procedure to exceed T_MAX_PROCEDURE_LEN.
The combined number of mode-0 steps and non-mode‑0 steps executed is equal to N_STEPS_MAX as described in [Vol 6] Part B, Section 4.5.18.1.
The number of CS subevents executed is equal to N_MAX_SUBEVENTS_PER_PROCEDURE.
If Channel Selection Algorithm #3b is used for non-mode-0 steps, and the channel map generated from CSFilteredChM has been used for CSNumRepetitions cycles for non-mode‑0 steps including the use for both Main_Mode and Sub_Mode steps.
If Channel Selection Algorithm #3c is used for non-mode-0 steps, and CSNumRepetitions invocations of Channel Selection Algorithm #3c have been completed for non-mode‑0 steps including the use for both Main_Mode and Sub_Mode steps.
For CS steps besides those in mode-0, a new channel shall be selected from the Channel Selection Algorithm #3 non-mode‑0 shuffled channel list each time a Main_Mode step is transmitted. The channel selected shall be re-used (i.e., not refreshed from the shuffled channel list content) when a subsequent mode‑1 Sub_Mode step is scheduled. If no subsequent mode‑1 Sub_Mode step is scheduled, a new channel shall be selected from the shuffled channel list for the Sub_Mode transmission. The channel selected shall also be re-used when repeating CS steps at the beginning of a CS subevent relative to the steps at the end of the previous CS subevent, as described in Section 4.4.
For mode-0 CS steps, a new channel shall be selected from the Channel Selection Algorithm #3 mode‑0 shuffled channel list each time a mode‑0 step is scheduled.
4.3. Channel Sounding steps
CS defines a set of interlocking transfers between two devices. The device initiating the CS procedures is known as the initiator, and the device responding to those procedures is known as the reflector. Within a CS procedure, CSStepCount shall be set to the CS step number, which starts at zero and is incremented by one at each subsequent step within that procedure, even if that step is not executed. CS steps are composed of a combination of modulated packets and modulated CS tones.
There are four different modes for the CS steps. Each of these modes has different usage goals: measuring frequency offset between devices (mode‑0), measuring round-trip times (mode‑1), measuring phase rotations due to distance (mode‑2), and measuring both round-trip times and phase rotations (mode‑3).
CS steps require a precise timing synchronization between the devices involved in the transactions (i.e., the initiator and the reflector). This timing synchronization is described in Section 4.5.
CS steps are separated by time periods that allow for performing a frequency hop. The structure is shown in Figure 4.3.

The time allowed for the frequency hop is known as T_FCS. The permitted values for T_FCS are shown in Table 4.3.
T_FCS Index | T_FCS | Mandatory/Optional/Conditional |
|---|---|---|
0 | 15 µs | O |
1 | 20 µs | O |
2 | 30 µs | O |
3 | 40 µs | C.1 |
4 | 50 µs | O |
5 | 60 µs | O |
6 | 80 µs | C.1 |
7 | 100 µs | O |
8 | 120 µs | O |
9 | 150 µs | M |
| ||
Within a CS procedure, the same T_FCS value shall be used for each of the frequency hops. Devices may use the T_FCS period to perform internal calibrations, in addition to performing the frequency change. Devices may also use this time period to allow settling of the next transmitted RF signal so that it has reached a stable state when the subsequent CS step begins.
During T_FCS, the output power of the reflector in the RF channel that is being switched to shall be at least 40 dB less than the output power to be used for transmissions by the reflector during the next CS step, as measured at the reflector’s antenna connector.
4.3.1. Channel Sounding step mode-0
CS step mode‑0 is used to measure the frequency offset between the initiator and the reflector at a given frequency. Devices supporting the CS feature shall implement CS step mode-0. Table 4.4 shows the structure for CS step mode‑0.
The CS initiator performs a measurement of the frequency offset of the transmitted RF signal from the CS reflector during CS step mode‑0. The CS initiator shall use this information to compensate for the frequency and timing error contributions in all further transmissions within subsequent CS steps in a CS subevent. For each CS subevent, the CS initiator shall report to the Host the frequency value used for this compensation. Requirements for this compensation are described in [Vol 6] Part A, Section 3.5.
Role/Duration | T_SY | T_RD | T_IP1 | T_SY + T_GD + T_FM | T_RD |
|---|---|---|---|---|---|
Initiator | CS_SYNC (CS_SYNC_0_I) | ramp down | |||
Reflector | CS_SYNC followed by a CS tone (CS_SYNC_0_R) | ramp down |
The initiator shall first transmit a CS_SYNC (CS_SYNC_0_I). The duration of the CS_SYNC (T_SY) corresponds to the definitions described in Section 2 and also depends on the CS_SYNC_PHY being used. The CS_SYNCs for mode‑0 shall not carry a sounding sequence or random sequence as part of the CS_SYNC.
After the transmission from the initiator is completed, a defined ramp-down window of 5 µs (T_RD) is allowed for the initiator to remove the transmitted energy from the RF channel. After T_RD, the output power from the initiator in the RF channel shall be at least 40 dB less than the output power used during the transmission of the CS_SYNC, as measured at the initiator’s antenna connector.
T_IP1 represents the idle time between the end of the transmission from the initiator and the start of the transmission from the reflector. Devices may use this time for internal calibrations if needed. The reflector may use this time to ramp up its transmitted signal, if necessary, in advance of the transmission of the CS_SYNC followed by a CS tone (CS_SYNC_0_R), which is described in Section 2.6. The permitted values for T_IP1 are shown in Table 4.5.
T_IP1 Index | T_IP1 | Mandatory/Optional/Conditional |
|---|---|---|
0 | 10 µs | O |
1 | 20 µs | O |
2 | 30 µs | O |
3 | 40 µs | C.1 |
4 | 50 µs | O |
5 | 60 µs | O |
6 | 80 µs | C.1 |
7 | 145 µs | M |
| ||
After T_IP1, the reflector shall transmit its CS_SYNC_0_R starting with the transmission of a CS_SYNC. The duration of the CS_SYNC (T_SY) depends on the CS_SYNC_PHY being used.
A guard time of T_GD length, as described in Section 2.6, then follows.
A frequency measurement period of T_FM follows next. The duration of T_FM for CS step mode‑0 shall be 80 µs.
After the transmission from the reflector is complete, a ramp-down window of T_RD shall be present using the same requirements as defined for the initiator.
The reflector may transmit its CS_SYNC_0_R even if it does not receive a CS_SYNC from the initiator or if the CS_SYNC was received with bit errors. The time duration of a CS step mode‑0 can be expressed as:
The set of values of the time of departure of the mode-0 packets sent by an initiator in a subevent is denoted here as ToDI[m], where m = 1, .., M and M is the number of mode‑0 steps in a subevent, and therefore ToDI[1] = 0. Within any subevent, the range of the set of values described by the set
shall be less than or equal to 0.25 µs.
4.3.2. Channel Sounding step mode-1
CS step mode-1 is used to measure the round-trip time between the initiator and the reflector. Devices supporting the CS feature shall implement CS step mode-1. Table 4.6 shows the structure defined for CS step mode‑1.
Role/Duration | T_SY | T_RD | T_IP1 | T_SY | T_RD |
|---|---|---|---|---|---|
Initiator | CS_SYNC (CS_SYNC_1) | ramp down | |||
Reflector | CS_SYNC (CS_SYNC_1) | ramp down |
The initiator starts by transmitting a CS_SYNC (CS_SYNC_1). The duration of the CS packet (T_SY) corresponds to the definitions described in Section 2 and also depends on the CS_SYNC_PHY being used. The CS_SYNCs for mode-1 may include a sounding sequence or random sequence as part of the CS_SYNC.
The transmission SNR output level may be adjusted during the CS_SYNC transmission. The permitted SNR output levels are described in [Vol 6] Part A, Section 3.1.3.
After the transmission from the initiator is completed, a defined ramp-down window of 5 µs (T_RD) is allowed for the initiator to remove the transmitted energy from the RF channel. After T_RD, the output power in the RF channel shall be at least 40 dB less than the output power used during the transmission of the CS_SYNC, measured at the initiator’s antenna connector.
T_IP1 represents the idle time between the transmission from the initiator and the transmission from the reflector. Devices may use this time for internal calibrations if needed. The reflector may use this time to ramp up its transmitted signal, if necessary, in advance of the transmission of the CS_SYNC. The duration of T_IP1 is defined in Section 4.3.1.
After T_IP1, the reflector transmits its CS_SYNC_1. Within this CS_SYNC, the presence or absence of a sounding sequence or random sequence, and the length of the sequence if present, shall match that of the intended initiator’s transmission.
The transmission SNR output level may be adjusted during the CS_SYNC transmission. The permitted SNR output levels are described in [Vol 6] Part A, Section 3.1.3.
After the transmission from the reflector is complete, a ramp-down window of T_RD shall be present using the same requirements as defined for the initiator.
The reflector may transmit its CS_SYNC_1 even if it does not receive a CS_SYNC from the initiator or if the CS_SYNC was received with bit errors. The time duration of a CS step mode‑1 can be expressed as:
Section 3.1 describes how round-trip time is computed using CS_SYNC exchanges. When reporting round-trip time to the Host, each device excludes nominal known time offsets from the reported time. This time is equivalent to the time period between the reception and transmission of the center of the CS_SYNC fields, T_SY_CENTER_DELTA. For CS step mode‑1, T_SY_CENTER_DELTA is equal to the following:
4.3.3. Channel Sounding step mode-2
CS step mode-2 is used to measure the phase rotations of the RF signal between the initiator and the reflector. Devices supporting the CS feature shall implement CS step mode‑2. Table 4.7 shows the structure defined for CS step mode‑2.
Role/Duration | (T_SW+T_PM)×(N_AP+1) | T_RD | T_IP2 | (T_SW+T_PM)×(N_AP+1) | T_RD |
|---|---|---|---|---|---|
Initiator | CS tone | ramp down | |||
Reflector | CS tone | ramp down |
The initiator transmits a CS tone. The duration of the CS tone shall be (T_SW+T_PM)×(N_AP+1), where T_PM is the Phase Measurement period, T_SW is the antenna switch duration, and N_AP is the number of antenna paths. The permitted values for T_PM are shown in Table 4.8.
T_PM Index | T_PM | Mandatory/Optional/Conditional |
|---|---|---|
0 | 10 µs | O |
1 | 20 µs | C.1 |
2 | 40 µs | M |
| ||
ASK modulation is employed during the CS tone extension slot (see Section 4.4). Here each N_AP set of T_PM length transmissions shall be followed by a single CS tone extension slot of the same T_PM length. This CS tone extension slot may carry a transmission. If a transmission is present, it shall be identical to that of the last T_PM slot and shall use the same antenna element used in that prior slot. If a transmission is not present in the CS tone extension slot, then that T_PM period shall still be present but shall not carry a transmission. The presence of a physical transmission in the extension transmission slot shall be seeded by the CS DRBG described in Section 4.8. The process of determining if a transmission is present is described in Section 4.4.
After the transmission from the initiator is completed, a defined ramp-down window of 5 µs (T_RD) is allowed for the initiator to remove the transmitted energy from the RF channel. After T_RD, the output power in the RF channel shall be at least 40 dB less than the output power used during the transmission of the CS tone, measured at the initiator’s antenna connector. This ramp-down window shall also apply directly after the initiator’s transmission is completed in the case where the CS tone extension slot does not carry an actual transmission. In this case, the period of T_RD shall still also be present after the CS tone extension slot and shall also not carry any added transmission from the initiator.
T_IP2 represents the idle time between the transmissions, including the CS tone extension slot from the initiator and the transmission from the reflector. Devices may use this time for internal calibrations, if needed. The reflector may use this time to ramp up its transmitted signal, if necessary, in advance of the transmission of the CS tone. Table 4.9 shows the permitted values for T_IP2. The T_IP2 value may be different from the T_IP1 value.
T_IP2 Index | T_IP2 | Mandatory/Optional/Conditional |
|---|---|---|
0 | 10 µs | O |
1 | 20 µs | O |
2 | 30 µs | O |
3 | 40 µs | C.1 |
4 | 50 µs | O |
5 | 60 µs | O |
6 | 80 µs | C.1 |
7 | 145 µs | M |
| ||
After T_IP2, the reflector transmits its CS tone. The duration of the CS tone shall be (T_SW+T_PM)×(N_AP+1), where T_PM is the Phase Measurement period, T_SW is the antenna switch duration, and N_AP is the number of antenna paths. The N_AP parameter is common to the entire CS procedure and is described in [Vol 6] Part A, Section 5.3. An extension transmission slot like the one that was present in the initiator to reflector direction shall immediately follow the last valid N_AP transmission. If a transmission is present, it shall be identical to the transmission of the last T_PM slot and shall use the same antenna element used in that prior slot. If a transmission is not present in the CS tone extension slot, then that T_PM period shall still be present but shall not carry a transmission. The presence of a physical transmission in the extension transmission slot shall be seeded by the CS DRBG described in Section 4.8. The process of determining if a transmission is present is described in Section 4.4.
After the transmission from the reflector is complete, a ramp-down window of T_RD shall be present using the same requirements defined for the initiator described above in this section. In the case where a transmission was not present in the CS tone extension slot, a period of T_RD shall still also be appended after the CS tone extension slot and shall also not carry any added transmission from the reflector.
The time duration of a CS step mode-2 can be expressed as:
For CS step mode-2, the time period between reception and transmission of the center of the CS tone at the antenna port is nominally expressed as:
4.3.4. Channel Sounding step mode-3
CS step mode-3 is used to measure the phase rotations of the RF signal and the round-trip time between the initiator and the reflector. Devices supporting the CS feature may optionally implement CS step mode-3. Table 4.10 shows the structure defined for CS step mode-3.
Role/Duration | T_SY+T_GD+(T_SW+T_PM)×(N_AP+1) | T_RD | T_IP2 | (T_SW+T_PM)×(N_AP+1) +T_GD+T_SY | T_RD |
|---|---|---|---|---|---|
Initiator | CS_SYNC followed by a CS tone (CS_SYNC_3_I) | ramp down | |||
Reflector | CS tone followed by a CS_SYNC (CS_SYNC_3_R) | ramp down |
The initiator transmits a CS_SYNC followed by a CS tone (CS_SYNC_3_I) as described in Section 2.6. The duration of the CS_SYNC (T_SY) corresponds to the definitions described in Section 2 and also depends on the CS_SYNC_PHY being used. The CS_SYNCs for mode‑3 may include a sounding sequence or random sequence as part of the CS_SYNC.
The transmission SNR output level may be adjusted during the CS_SYNC transmission. The permitted SNR output levels are described in [Vol 6] Part A, Section 3.1.3.
A guard time of T_GD length, as described in Section 2.6, then follows.
The duration of the CS tone shall be (T_SW+T_PM)×(N_AP + 1), where T_PM is the phase measurement period and N_AP is the number of antenna paths. The valid values for the T_PM parameter are described in Section 4.3.3.
ASK modulation is employed during the CS tone extension slot (see Section 4.4). Here each N_AP set of T_PM length transmissions shall be followed by a single CS tone extension slot of the same T_PM extent. This CS tone extension slot may or may not carry a transmission. If a transmission is present, it shall be identical to that of the last T_PM slot and shall use the same antenna element used in that prior slot. If a transmission is not present in the CS tone extension slot, then that T_PM period shall still be present but shall not carry a transmission. The presence of a physical transmission in the extension transmission slot shall be seeded by the CS DRBG described in Section 4.8. The process of determining if a transmission is present is described in Section 4.4.
After the transmission from the initiator has completed, a defined ramp-down window of 5 µs (T_RD) is allowed for the initiator to remove the transmitted energy from the RF channel. After T_RD the output power in the RF channel shall be at least 40 dB less than the output power used during the transmission of the CS_SYNC measured at the initiator’s antenna connector. This ramp-down window shall also apply directly after the initiator’s transmission is completed in the case where the CS tone extension slot does not carry an actual transmission. In this case, the period of T_RD shall still be present after the CS tone extension slot and shall also not carry any added transmission from the initiator.
T_IP2 represents the idle time between the transmission from the initiator and the transmission from the reflector. Devices may use this time for internal calibrations if needed. The reflector may use this time to ramp up its transmitted signal, if necessary, in advance of the transmission. The duration of T_IP2 is defined in Section 4.3.3.
After T_IP2, the reflector transmits a CS tone followed by a CS_SYNC (CS_SYNC_3_R) as described in Section 2.6. This sequence begins with the transmission of the CS tone. The duration of the CS tone shall be either (T_SW+T_PM)×N_AP or (T_SW+T_PM)×(N_AP + 1) depending on whether a transmission is selected for the CS tone extension slot. If a transmission is present, it shall be identical to that of the last T_PM slot and shall use the same antenna element used in that prior slot. If a transmission is not present in the CS tone extension slot, then that T_SW+T_PM period shall not be present but shall be compensated for as described below. The presence of a physical transmission in the extension transmission slot shall be seeded by the CS DRBG described in Section 4.8. The process of determining if a transmission is present is described in Section 4.4.
A guard time of T_GD length as described in Section 2.6 then follows.
The reflector may then transmit its CS_SYNC. Within this CS_SYNC, the presence or absence of a sounding sequence or random sequence, and the length of the sequence if present, shall match that of the initiator’s transmission.
The transmission SNR output level may be adjusted during the CS_SYNC transmission. The permitted SNR output levels are described in [Vol 6] Part A, Section 3.1.3.
A T_PM period without a physical transmission shall be inserted directly after the reflector’s CS_SYNC transmission if the CS tone extension slot was not present during the prior CS tone transmission. This T_PM period shall be accompanied by a T_SW period as if it had occurred before the CS_SYNC transmission.
After the transmission from the reflector is complete, a ramp-down window of T_RD shall be present using the same requirements defined for the initiator described above in this section. In the case where a transmission was not present in the CS tone extension slot, a period of T_RD shall also be appended after the CS tone extension slot and shall also not carry any added transmission from the reflector.
The time duration of a CS step mode-3 can be expressed as:
Section 3.1 describes how round-trip time is computed using CS_SYNC exchanges. When reporting round-trip time to the Host, each device excludes nominal known time offsets from the reported time. This time is equivalent to the time period between the reception and transmission of the center of the CS_SYNC fields, T_SY_CENTER_DELTA. For CS step mode‑3, T_SY_CENTER_DELTA is equal to the following:
T_SY_CENTER_DELTA = TSY + TRD + 2 x TGD + 2 x (TSW + TPM ) x NAP + 2 x (TSW + TPM ) + TIP2, if a physical transmission is present in the reflector to initiator transmission extension slot.
Otherwise, T_SY_CENTER_DELTA = TSY + TRD + 2 x TGD + 2 x (TSW + TPM ) x NAP + (TSW + TPM ) + TIP2.
For CS step mode-3, the time period between reception and transmission of the center of the CS tone at the antenna port is nominally expressed as:
T_PM_CENTER_DELTA = (TPM + TSW) × (NAP + 1) + TSY + TGD + TRD + TIP2
4.4. Channel Sounding subevent and mode sequencing
CS subevents have a maximum duration of T_SUBEVENT_LEN, as described in [Vol 6] Part B, Section 4.5.18.1. Each subevent contains a varying number of CS steps. The number of steps included in a subevent depends on the varying step combinations used in that subevent.
4.4.1. Tone extension slots
For CS tones, each T_PM transmission shall be followed by a CS tone extension slot as described in Section 4.3.3 and Section 4.3.4. The presence of an actual transmission in this CS tone extension slot shall be selected at random, seeded by the CS DRBG described in Section 4.8.
CS DRBG shall be invoked to generate a single random bit (see Section 4.8). If this bit is set to 1, then a physical transmission shall be present in the CS tone extension slot. If this bit is set to 0, then no transmission shall be present in the CS tone extension slot. Even without a transmission, the CS tone extension slot shall still be present. Refer to Section 4.3.3 and Section 4.3.4 for information about the CS tone extension slot and its positioning within each step.
Figure 4.4 shows a sequence of four CS steps, each of type mode‑2, with the CS tone extension slot transmission determined by the output of the CS DRBG.

Likewise, Figure 4.5 shows a sequence of four CS steps, each of type mode-3, with the CS tone extension slot transmission determined by the output of the CS DRBG. The position of the CS tone extension slot for mode-3 steps is described in Section 4.3.4.
Refer to Section 4.8 for CS DRBG invocation ordering rules.
4.4.2. CS subevent structure
Within a CS subevent, if the cumulative duration of a CS step exceeds T_SUBEVENT_LEN as described in [Vol 6] Part B, Section 4.5.18.1, then the CS subevent shall be closed, and that CS step shall occur in the next scheduled CS subevent directly after the initial mode‑0 steps and after any Main_Mode Repetitions (see Section 4.2).
A CS subevent starts with one or more mode-0 steps defined by CSMode0Steps. A series of subsequent non-mode‑0 steps shall follow in the same subevent. Any CS procedure shall include the use of no more than two non-mode‑0 modes, the Main_Mode and the Sub_Mode. An example of this sequencing is shown in Figure 4.6.
For non-mode-0 steps, Main_Mode and Sub_Mode combinations shall be selected from the valid combinations defined in Table 4.11.
Main_Mode | Sub_Mode |
|---|---|
Mode-1 | None |
Mode-2 | None |
Mode-3 | None |
Mode-2 | Mode-1 |
Mode-2 | Mode-3 |
Mode-3 | Mode-2 |
4.4.3. Sub_Mode insertion
The following rules shall apply for Sub_Mode insertion only when a Sub_Mode has been selected for a CS procedure. These rules shall repeat for the entire CS procedure.
Sub_Mode insertion is the process of sequencing the occurrence of the Main_Mode steps and the Sub_Mode steps. This sequencing is performed irrespective of the occurrence of CS subevent boundaries and shall use the following parameters:
Main_Mode_Min_Steps – the minimum number of Main_Mode steps that shall occur before the occurrence of a single Sub_Mode step.
Main_Mode_Max_Steps – the maximum number of Main_Mode steps that shall occur before the occurrence of a single a Sub_Mode step.
The exact number of Main_Mode steps that occur before a Sub_Mode step insertion shall be randomized for each sequence. The random number generation function hr1 (see Section 4.8.1) is invoked to determine the randomized number of Main_Mode steps that occur in the sequence.
The number of Main_Mode steps to execute shall be calculated as follows.
hr1( Main_Mode_Max_Steps – Main_Mode_Min_Steps + 1 ) + Main_Mode_Min_Steps
The number of Main_Mode steps to execute before a Sub_Mode insertion shall be generated at the CS step where the first Main_Mode step within that sequence occurs. Refer to Section 4.8 for CS DRBG invocation ordering rules.
4.4.4. Main_mode repetition
After a CS subevent, a variable number of Main_Mode steps and their respective transmission channels may be optionally repeated in the next CS subevent directly after the mode-0 transmissions. The Main_Mode_Repetition value from the CS configuration selected (see [Vol 6] Part B, Section 2.4.2.45) for a CS procedure shall denote the number of Main_Mode steps that are repeated from the end of one CS subevent to the beginning of the next.
When CS steps are repeated based on the Main_Mode_Repetition value, only the channel index and Main_Mode type shall be repeated in the next CS subevent. All other aspects that involve seeding from the CS DRBG shall be newly generated in the steps that are repeated. If the value of Main_Mode_Repetition is greater than 1, then the repeated steps in the next CS subevent shall be in the same order as in the previous CS subevent.
Only CS steps from the current subevent that were not repeated from the last subevent shall be repeated in the next subevent. If the number of CS steps that are candidates to be repeated from the current subevent into the next subevent is less than the Main_Mode_Repetition value, then only those CS steps shall be repeated in the next subevent.
Sub_Mode insertion, if present, shall be calculated as if the Main_Mode_Repetition value were specified as zero. This is equivalent to not counting the occurrences resulting from Main_Mode_Repetition when determining where the Sub_Mode insertion occurs. The step placement due to Main_Mode_Repetition shall occur first within a CS subevent in the case of pending step placement due to Sub_Mode insertion.
4.4.5. Channel Sounding procedure and procedure repeat desynchronization
A CS subevent will always start with the exchange of one or more mode‑0 steps, as described in Section 4.4.2. Within each of these mode‑0 steps is a CS_SYNC exchange as described in Section 4.3.1. A mode‑0 exchange is considered successful in the case where both Link Layers properly receive a CS_SYNC PDU with an access address quality indication result of 0 or 1, as described in Section 2.2.2. Alternatively, a mode‑0 step exchange is considered lost when either link layer fails to receive a CS_SYNC PDU or the resulting access address quality indication result is greater than 1, within that mode‑0 step. In the case that all mode‑0 steps within a CS subevent are lost, then that CS subevent is also considered lost.
[Vol 6] Part B, Section 4.2.4 describes the window widening recommendations for synchronization of the first CS subevent within a CS event. If the first consecutive CS subevents within a CS event are lost, then these window widening recommendations apply to the next sequential CS subevent within that CS event as if that CS subevent was the first in occurrence within that CS event.
If the first CS subevent(s) within any CS event is lost, then it is implementation dependent if an attempt is made to synchronize with the next CS subevent within that CS event. In this case, if synchronization with a CS event is abandoned, then that CS event is similarly considered lost. In the case that an entire CS procedure is abandoned due to the first consecutive CS events within that procedure being lost, then that CS procedure is also considered lost.
In the case that CS procedure instances are actively running and N_PROCEDURE_LOST=2 consecutive CS procedure repeat instances are lost, then a Link Layer should initiate the Channel Sounding Procedure Repeat Termination procedure, as described in [Vol 6] Part B, Section 5.1.27.
4.5. Timing of steps
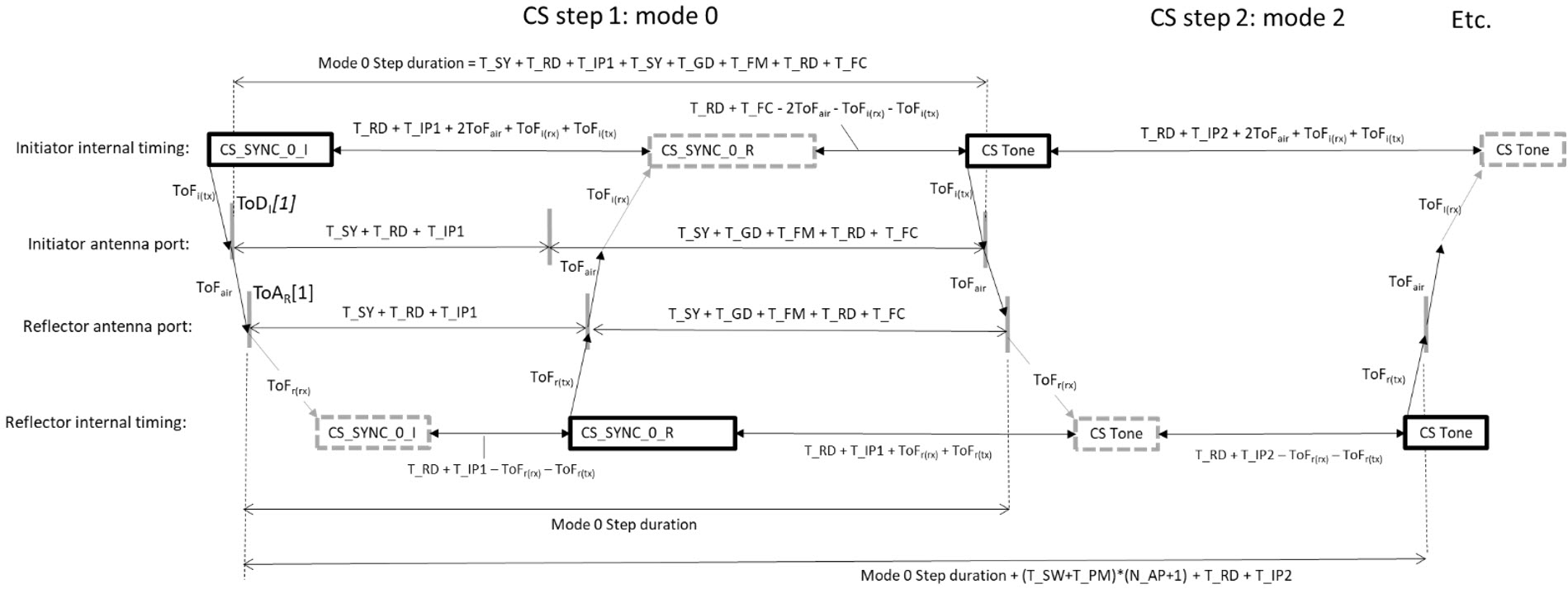
Figure 4.7 shows an example of the timing of CS steps when a single antenna is in use. All timings in Figure 4.7 are based on the reflector’s timing reference. ToDI[k] represents the time of departure of the packet at the initiator’s antenna port sent in the kth step within a subevent, if such a packet exists within that step. ToAR[k] represents the time of arrival at the reflector’s antenna port of the packet sent in the kth step within a subevent, if such a packet exists within that step. ToFair represents the time of flight between antenna ports. ToFi and ToFr represent the initiator and reflector circuit delay, respectively. In Figure 4.7, solid boxes denote transmission times and dashed grey boxes denote reception windows.
The initiator shall align its transmission timings relative to the start of its first mode-0 transmission at its antenna port, TODi[1] (see Figure 4.7), based on the reflector’s clock reference as follows:
where is the nominal start time of each transmission according to its local clock reference and FFO[1] is the FFO estimated from the first mode-0 CS tone (see [Vol 6] Part A, Section 3.5.1). The initiator should adjust its CS tone reception window to compensate for the round-trip time of flight between devices and to compensate for any relevant known synchronization errors or internal circuit delays so that its phase center of measurement falls in the center of the received CS tone (see [Vol 6] Part A, Section 6.4).
The reflector shall calculate all transmission timings relative to the time of arrival of a mode-0 packet at its antenna port, using its own timing reference ToAr[m] (see Figure 4.7), where m is assumed to be the first successfully received mode-0 packet. The reflector’s timing reference, defined by the frequency of the first transmitted mode-0 packet CS tone, shall be constant throughout a subevent, and the reflector shall not perform any timing adjustment of its transmissions to compensate for the clock frequency offset between devices. The reflector should adjust its CS tone reception window to compensate for known synchronization errors or internal circuit delay so that its phase center of measurement falls in the center of the received CS tone (see [Vol 6] Part A, Section 6.4).
Both initiator and reflector shall maintain an accuracy of ±1 µs in the timing of their transmissions as described in this section.
4.6. Phase measurements during T_PM
Devices perform phase measurements during T_PM. Devices shall perform N_AP + 1 phase measurements for each of the phase measurement periods during a mode‑2 or mode‑3 step, one for each of the antenna paths as well as for the CS tone extension slot. The rules for T_PM measurements taken over tone extension slots are described below.
Each T_PM period shall start and end with at least a 1 µs exclusion period, as shown in Figure 4.8, to allow for peer device timing error (see Section 4.5). A longer exclusion period should be introduced as necessary to compensate for local device timing accuracy. These exclusion periods shall not be considered as valid regions for PCT extraction. PCT sampling is described in [Vol 6] Part A, Section 6.4 and Section 4.5.
 |
Each measurement within T_PM results in a single PCT value expressed as complex number I+jQ. When a CS subevent contains multiple CS steps, devices should maintain receiver characteristics (e.g., receiver’s gain and latency across T_PM periods should remain constant across the CS steps). If this is not possible, receivers should be able to make adjustments to the resulting measurements to emulate this constant behavior.
The IQ terms shall each use 12 bits to encode their value.
In addition to the IQ values, devices shall provide a reference power level (RPL) in dBm. The RPL shall be encoded as an 8-bit signed number. The RPL expressed in dBm shall correspond to the power of a hypothetical PCT value whose amplitude is a constant value of 2048. A single RPL is used for all the PCT values in a CS subevent.
The conversion between IQ values as unitless values to power in dBm can be expressed as:
Devices may assign a tone quality indication to each of the PCT measurements. The tone quality indication shall be a 2-bit number with definitions as shown in Table 4.12. Devices that are not able to compute a quality indication shall report a value of 3.
The following definitions pertain to devices that are capable of computing tone quality indications.
Value | Tone Quality |
|---|---|
0 | High quality |
1 | Medium quality |
2 | Low quality |
3 | Quality indication not available / unknown quality |
The following shall be tested with a T_PM value of 40 µs.
Devices shall report high quality when the signal at the antenna port is a CS tone of -67 dBm, with a Gaussian noise floor of -151 dBm/Hz or less. This reported value shall be the outcome of the measurement for 90% of the CS tones and under all valid frequency offsets of the input signal, as described in [Vol 6] Part A, Section 3.5.2.
Devices shall report low quality when the signal at the antenna port is a CS tone of -67 dBm with a Gaussian noise floor of -133 dBm/Hz or greater. This reported value shall be the outcome of the measurement for 90% of the CS tones and under all valid frequency offsets of the input signal, as described in [Vol 6] Part A, Section 3.5.2.
Devices may optionally report medium quality when the received signal is between the good quality and low quality thresholds.
The use of Gaussian noise signals to represent channel impairments is intended to represent external sources of wideband interference.
In tone extension slots, no T_PM measurement shall occur in a mode-3 step in the reflector to initiator direction when a CS tone extension slot transmission is not present. Instead, an empty T_PM measurement result shall take the place of the T_PM measurement. In any other case of a CS tone extension, the T_PM measurement over that tone extension slot shall be reported.
An empty T_PM measurement shall be defined with IQ values each set to zero and with a tone quality indication set to “quality indication not available”.
4.7. Phase measurements with antenna switching
During CS tone exchanges, the initiator switches to the intended antenna element and transmits its CS tone first and the reflector performs phase measurements. Then, after a T_RD + T_IP2 period, the reflector switches to the intended antenna element and transmits its CS tone, and the initiator performs phase measurements. The configuration options listed in [Vol 6] Part A, Section 5.3 affect how the switching happens, which antenna is selected during the execution within a CS step, and whether the switch applies to the outgoing signal (i.e., switch on transmitted RF signal), or the incoming signal (i.e., switch on received RF signal), or both.
Antenna switching occurs just before the start of every T_PM period for each configuration with multiple antenna paths. T_SW is the switch period time and is reserved for antenna switching, irrespective of whether the antenna to be switched is a local antenna or a remote antenna. During the period when an antenna is switched, the signal might not be stable and shall not be used for measurements. The T_SW duration is local device specific and each peer shall indicate its own preferred setting, as described in [Vol 6] Part B, Section 5.1.24. When antenna switching is performed, the duration of T_SW shall be 1, 2, 4, or 10 µs. When no antenna switching is performed (e.g., in the 1:1 configuration), the value of T_SW shall be set to 0. Devices switching transmitting antennas must control switching transients according to the requirements specified in Part A.
The value of T_SW used in a CS procedure depends on the antenna switch configuration selected for that procedure, as described in the following subsections.
4.7.1. Antenna switching in the 1:1 configuration
There shall not be antenna switching activity in the 1:1 configuration.
4.7.2. Antenna switching in the N_AP:1 configuration
In the N_AP:1 configuration, only the initiator performs antenna switching. Figure 4.9 shows the procedure. In the figure, * represents the extension slot that can occur as shown, or can occur after T_SY, specifically for a mode‑3 step.
In this configuration, with N_AP antennas in the initiator, the initiator shall be the only device performing antenna switching. The antenna switch duration selected shall be the T_SW value of the initiator.
During its transmission phase, the initiator shall perform N_AP antenna switches. Each switch shall be performed before the start of the T_PM period.
During its reception phase, the initiator shall perform N_AP antenna switches. Each switch shall be performed before the start of the T_PM period.
The reflector shall not perform antenna switching in this configuration. The reflector shall not perform any measurements during the switch duration of the initiator.
The antenna switching sequence that the initiator selects for each T_PM period during its transmission phase shall be identical to the antenna switching sequence used during its reception phase.
Figure 4.9 shows the antenna switch procedure for a 3:1 antenna switch configuration, including the antenna path extension slot described in Section 4.4. For a mode‑3 step in the reflector-to-initiator direction, the last T_SW period and associated antenna extension slot (indicated by * in Figure 4.9) shall occur after the last T_PM period and before the CS_SYNC packet as described in Section 4.3.4.
4.7.3. Antenna switching in the 1:N_AP configuration
In the 1:N configuration, only the reflector performs antenna switching. Figure 4.10 shows the procedure. In this figure, * represents the extension slot that can occur as shown or can occur after T_SY.
 |
In this configuration, with N_AP antennas in the reflector, the reflector shall be the only device performing antenna switching. The antenna switch duration selected shall be the T_SW value of the reflector.
During its reception phase, the reflector shall perform N_AP antenna switches. Each switch shall be performed before the start of the T_PM period.
During its transmission phase, the reflector shall perform N_AP antenna switches. Each switch shall be performed before the start of the T_PM period.
The initiator shall not perform antenna switching in this configuration. The initiator shall not perform any measurements during the switch duration of the reflector.
The antenna switching sequence that the reflector selects for each T_PM period during its transmission phase shall be identical to the antenna switching sequence used during its reception phase.
Figure 4.10 shows the antenna switch procedure for a 1:3 antenna switch configuration, including the antenna path extension slot as described in Section 4.4. For a mode‑3 step in the reflector-to-initiator direction, the last T_SW period and associated antenna extension slot (indicated by * in Figure 4.10) may occur as shown in the figure or may occur after T_SY as described in Section 4.3.4.
4.7.4. Antenna switching in the 2:2 (N_AP = 4) configuration
In the 2:2 (N_AP = 4) configuration, both devices perform antenna switching. At each antenna switch point, one device or both devices simultaneously may perform antenna switching. Figure 4.11 shows the procedure. In this figure, * represents the extension slot that can occur as shown or can occur after T_SY.

For the 2:2 antenna switch procedure, each antenna path consists of a combination of antennas selected by both the initiator and reflector, as described in [Vol 6] Part A, Section 5.3.
During its transmission phase, the initiator shall perform an antenna switch for before the first T_PM interval and then may perform an antenna switch at each subsequent T_PM interval, depending on the antenna path selected for that interval. Each switch shall be performed immediately before the start of the T_PM period.
Similarly, during its reception phase, the reflector shall perform an antenna switch for the first T_PM interval and then may perform an antenna switch at each subsequent T_PM interval, depending on the antenna path selected for that interval. Each switch shall be performed immediately before the start of the T_PM period.
During its reception phase, the initiator shall perform an antenna switch for the first T_PM interval and then may perform an antenna switch at each subsequent T_PM interval, depending on the antenna path selected for that interval. Each switch shall be performed immediately before the start of the T_PM period.
Similarly, during its transmission phase, the reflector shall perform an antenna switch for the first T_PM interval and then may perform an antenna switch at each subsequent T_PM interval, depending on the antenna path selected for that interval. Each switch shall be performed immediately before the start of the T_PM period.
The antenna switch duration selected for all required antenna element switching shall be the larger of the T_SW values of the initiator and the reflector. The device acting as the receiver shall not perform any measurements during the switch duration of the device acting as the transmitter.
The antenna switching sequence that the initiator and reflector select for each T_PM period during the first part of the CS step (initiator to reflector) shall be identical to the antenna switching sequence used during the second part of the CS step (reflector to initiator).
Figure 4.11 shows the antenna switch procedure for a 2:2 antenna switch configuration, including the antenna path extension slot described in Section 4.4. For a mode‑3 step in the reflector-to initiator-direction, the last T_SW period and associated antenna extension slot (indicated by * in Figure 4.11) may occur as shown in the figure or may occur after T_SY, as described in Section 4.3.4.
4.7.5. Antenna path permutations
During antenna switching, the antenna path position ordering in a CS tone exchange shall be randomized. Each antenna path is described in [Vol 6] Part A, Section 5.3, where the initiator is device A and the reflector is device B.
Each device may switch between up to four antenna paths within a CS step. The randomized antenna path permutation in a CS step shall be selected using the random number generation function hr1 (see Section 4.8.1). The number of antenna paths used within the permutation is the maximum number of N_AP antenna paths, as described in [Vol 6] Part A, Section 5.3.
When N_AP is greater than 1, the antenna path permutation index shall be calculated as follows:
hr1( N_AP! )
See Section 4.8 for CS DRBG invocation ordering rules.
An antenna path permutation index is used to look up the specific antenna path position order used at each step that contains a CS tone exchange within a CS step. These lookup tables are defined based on the number of antenna paths being used.
If N_AP = 2, then Table 4.13 shall be used to select the antenna path permutation.
Antenna Path Permutation Index | Antenna Path Positions After Permutation |
|---|---|
0 | A1 A2 |
1 | A2 A1 |
If N_AP = 3, then Table 4.14 shall be used to select the antenna path permutation.
Antenna Path Permutation Index | Antenna Path Positions After Permutation |
|---|---|
0 | A1 A2 A3 |
1 | A2 A1 A3 |
2 | A1 A3 A2 |
3 | A3 A1 A2 |
4 | A3 A2 A1 |
5 | A2 A3 A1 |
If N_AP = 4, then Table 4.15 shall be used to select the antenna path permutation.
Antenna Path Permutation Index | Antenna Path Positions After Permutation |
|---|---|
0 | A1 A2 A3 A4 |
1 | A2 A1 A3 A4 |
2 | A1 A3 A2 A4 |
3 | A3 A1 A2 A4 |
4 | A3 A2 A1 A4 |
5 | A2 A3 A1 A4 |
6 | A1 A2 A4 A3 |
7 | A2 A1 A4 A3 |
8 | A1 A4 A2 A3 |
9 | A4 A1 A2 A3 |
10 | A4 A2 A1 A3 |
11 | A2 A4 A1 A3 |
12 | A1 A4 A3 A2 |
13 | A4 A1 A3 A2 |
14 | A1 A3 A4 A2 |
15 | A3 A1 A4 A2 |
16 | A3 A4 A1 A2 |
17 | A4 A3 A1 A2 |
18 | A4 A2 A3 A1 |
19 | A2 A4 A3 A1 |
20 | A4 A3 A2 A1 |
21 | A3 A4 A2 A1 |
22 | A3 A2 A4 A1 |
23 | A2 A3 A4 A1 |
Figure 4.12 shows four successive mode-2 CS steps that use a different antenna path permutation index at each step. In this figure, extension slot transmissions are present in the first and third steps.
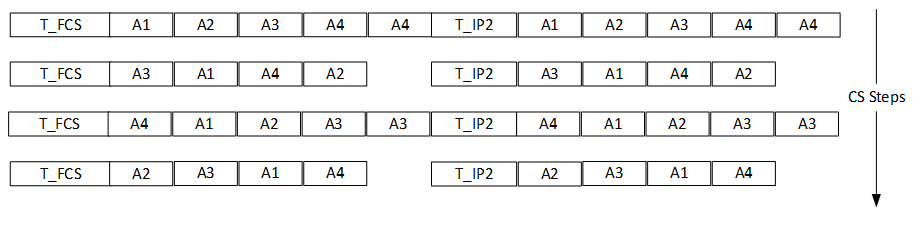
4.8. Channel Sounding random bit generation
A dedicated Channel Sounding Deterministic Random Bit Generator (CS DRBG) is used to coordinate the randomization of several transaction types during a CS procedure. These transaction types are identified by the value of the transaction identifier type, as shown in Table 4.16. CSTransactionID represents the transaction identifier being processed by the CS DRBG. The toolbox function CS_DRBG, which is invoked for random bit generation, is described in [Vol 6] Part E, Section 3.1.6.
Transaction Identifier (CSTransactionID) | Transaction Description |
|---|---|
0x00 | Randomization of hop channel set for non-mode‑0 steps. Described in Section 4.1. |
0x01 | Randomization of hop channel set for mode‑0 steps. Described in Section 4.1. |
0x02 | Randomization of subevent Sub_Mode (into Main_Mode cycle). Described in Section 4.4. |
0x03 | T_PM CS tone extension slot transmission presence. Described in Section 4.4. |
0x04 | Antenna path permutation index selection. Described in Section 4.7.5. |
0x05 | CS Access Address generation. Described in Section 2.2.1. |
0x06 | Sounding sequence marker position randomization. Described in Section 2.4. |
0x07 | Sounding sequence marker signal selection. Described in Section 2.4. |
0x08 | Random sequence generation. Described in Section 2.5. |
0x09 | Backtracking resistance. Described in [Vol 6] Part E, Section 3.1.7. |
Each of the transactions listed in Table 4.16 uses a fresh set of random bits at different points within a CS procedure. Each transaction might use a different number of random bits, which might be less than the 128-bit generation output of the CS DRBG. If all bits are not used during a transaction, the remaining bits shall be preserved and used in subsequent transactions until there are not enough remaining bits to complete the transaction. At this point, the remaining bits shall be discarded and a new set of 128 random bits shall be generated.
A newly generated set of random bits might not be needed at each CS step, either because there are still an adequate number of remaining unused bits from a previous DRBG invocation for that specific transaction identifier, or because there is no need for random bit usage for the specific CS mode for that CS step.
For example, if a transaction identifier uses random bits in 8-bit quantities at each step, then at step 0 the DRBG would be invoked to provide 128 bits of random bit output. The first eight bits would be used at step 0, and the remaining 120 bits would be used in 8-bit quantities at each subsequent step through step 15. At step 16, because not enough bits are available to complete the step, a fresh set of 128 random bits is generated and the distribution process of those bits is repeated.
When a new set of 128 random bits is generated, the CS Step_Counter described in [Vol 6] Part E, Section 3.2.2 shall be set to the value of the CS step that is being processed, with the following exceptions:
When used for Channel Selection Algorithm #3c as described in Section 4.1.4.2, the CS Step_Counter as described in [Vol 6] Part E, Section 3.2.2 shall be set to 0.
A transaction counter represented by CSTransactionCounter and used in the CS Transaction_Counter described in [Vol 6] Part E, Section 3.2.2 shall be incremented if a specific transaction ID uses multiple quantities of 128 random bits at any one step. CSTransactionCounter shall always begin with a value of 0 the first time a new set of 128 random bits is generated at any CS step for a specific transaction ID.
The order in which the CS DRBG is invoked is critical to maintain synchronization with the peer CS device. The CS DRBG, when used for the purposes of generating random bits for each transaction identifier listed in Table 4.16, shall be invoked with the following ordered rules:
By CS steps – In sequential order of CS steps in a CS procedure and subevents, from first to last.
By device role – Values used by the initiator shall be generated first, followed by those used by the reflector.
By transaction type – In the transmission order of a function using a specific transaction type, if random bits for that transaction type are used more than once within any single CS step.
4.8.1. Channel Sounding random number generation function hr1
Within a CS procedure, there are several instances where the CS DRBG is used to seed random number generation with different range sets for the specific transaction types described in Section 4.8. Seeding of random number generation in a uniform distribution within a range is directly supported by the CS DRBG when the range is a power of 2. For other arbitrary ranges, the following description in this section shall be used.
Distribution bias in the random number generation procedure is mitigated with a two-step approach. First, the initial seeding input from the CS DRBG is checked for bias potential. Next, if a bias potential is detected, a supplemental bit draw from the CS DRBG is performed to extend the granularity of the random number generation process.
N_CS_RANGE_GEN_RANDOMIZED_BITS is the number of randomly generated bits used to perform the randomization seeding process. This value is fixed at 8 bits.
The CS random number generation function hr1 is used to generate random numbers within an arbitrary range. The input to hr1 is an 8-bit unsigned integer R, representing the arbitrary range 0 to R-1 from which a random number is to be generated. This value shall be greater than 0 and less than or equal to 255.
The following value is returned from hr1:
Rout is an 8-bit unsigned integer.
The following temporary value is used:
Trand is a 16-bit unsigned integer.
The input/output format of hr1 is as follows:
Rout = hr1( R )
hr1 processing is as follows:
If ( R == 1 ) | ||
then return 0 | ||
Trand = R x CS_DRBG( N_CS_RANGE_GEN_RANDOMIZED_BITS ) | ||
if ( Trand AND 0xFF ) < ( 256 % R ) | ||
else | ||
return Rout | ||